In today’s post, we are going to work on proportions. This time we will look at a way of solving direct and inverse proportions: the rule of 3.
What is the rule of 3?
The rule of 3 is an operation that helps us quickly solve both direct and inverse proportion word problems.
In order to use the rule of 3, we need three values: two that are proportional to one another and a third. From there, we will figure out the fourth value.
Direct rule of 3
We will begin by looking at how to apply it in the case of direct proportions.
We will place the 3 values (which we will call “a”, “b”, and “c”) and the unknown value that we want to figure out (“x”) in a table. Next, we will apply the following formula:
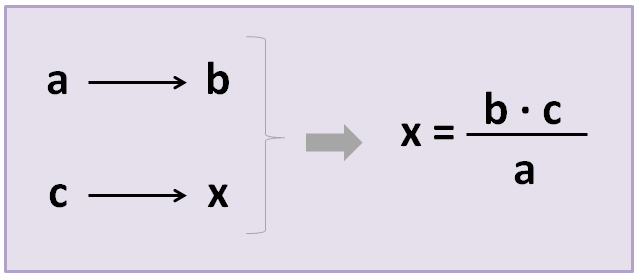
We are going to solve the following problem as an example:

Upon arriving at the hotel, the staff gave us a map displaying the places of interest in the city and told us that 5 centimeters on the map represented 600 meters in reality. Today we want to go to a park that is located 8 centimeters from the hotel on the map. How far from the hotel is the park?
Let’s make a table with the 3 values and the unknown value (“x”), and we will find “x” with the formula that we have just learned.
Centimeters on the map Meters in reality
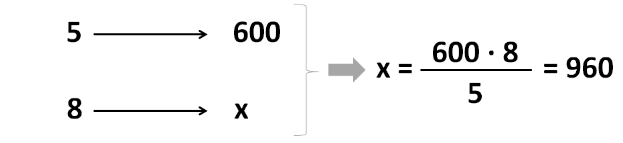
Answer: The park is located 960 meters from the hotel.
Inverse Rule of 3
Now we will look at how to apply the rule of 3 in the case of inverse proportions.
We will place the 3 values and the unknown value in the table, just as we did in the previous case, but we will apply a different formula:
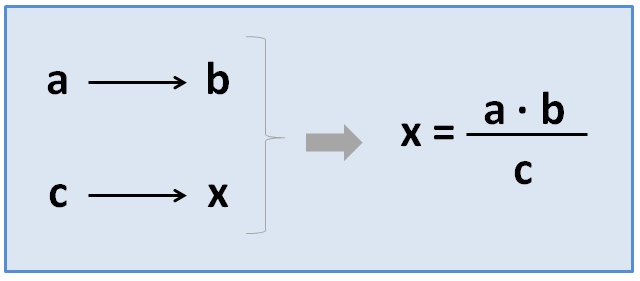
Let’s look at an example:

Yesterday, 2 trucks transported goods from the port to the warehouse. Today, 3 trucks, the same size as yesterday, will have to make 6 trips to transport the same amount of goods from the warehouse to the mall. How many trips did the trucks make yesterday?
We place the values in a table and apply the formula for the inverse rule of 3:
Trucks Trips Necessary
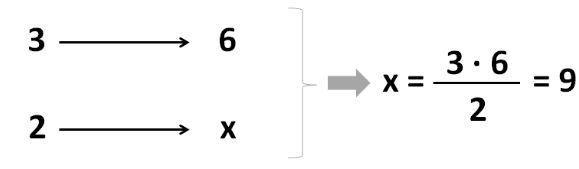
Answer: Yesterday, 2 trucks made 9 trips.
What did you think of this post? Isn’t it easy to apply the rule of 3 to proportion word problems!
You can learn more about direct and inverse proportion with this previous post on our blog: Rule of Three Problems.
Remember that you will be able to practice exercises, proportion word problems and much more with Smartick! Try it for free!
Learn More:
- Direct and Inverse Proportionality Problems
- Direct and Inverse Rule of 3 Problems
- Inverse Proportionality: The Rule of Three Inverse
- Problems Involving the Inverse Rule of 3
- Compound Rule of 3: When to Use It and Some Problems








Multiplication is vexation, division is as bad.
The rule of three perplexes me and practice drives me mad!
I’ve wondered for decades what the heck the “Rule of Three” was. Thank you for a translation elementary enough, and with examples’, to make it possible for me to comprehend. Thank you!
I realy don’t have words to show my happiness after reading this blog. Thank you so much!
These examples are quite good. The second and the third one really helped me!!
still want to know more.
I have 3 children. Can you please send me more information regarding your fees (per hour and per month) for Grade 4, Grade 7 and Grade 12 (Maths & Science). I prefer communication via email please.
Hi Danita,
Smartick has monthly, quarterly and annual subscriptions, with the option to choose between one full installment or monthly payments for the year commitment. We do not have subscriptions based on hours or days.
The price depends on the number of students you subscribe and the duration of your commitment.
Smartick adapts to each student´s level regardless of their age or grade.
I have asked my colleagues to contact you via email to clarify any questions you may have. You can also contact them at [email protected]
Thanks!
This example doesn’t show why it works or how to differentiate one formula versus the other. Understanding the relationship between the numbers is key, and this doesn’t even touch in that.
Hi Cindy,
Thanks for your comment! We previously published a blog post on direct and inverse proportions with some problems, which describes how to identify and differentiate them in more detail. We’ve edited the Rule of Three post to include a link to it, you can read it by clicking here: https://www.smartickmethod.com/blog/math/ratios-and-proportional-relationships/rule-of-three-problems/