In today’s post, we are going to learn how to solve multiplication problems using an area model. You will see how simple it is to understand this multiplication algorithm.
Earlier with Smartick, we saw that we can represent multiplication with a rectangle whose sides have multiplication factors.
Today I will teach you the area model, based on the distributive property of multiplication.
I am going to show you an example so that you can use this model to solve any multiplication problems you want.
Example of multiplication problem with the area model
We are going to look at how to solve the multiplication problem 24 x 35.
To begin, you need to represent this multiplication on a rectangle with sides 24 and 35:
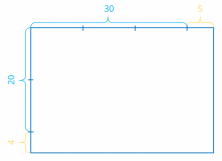 Now draw several rectangles marking each part separately in order to separate the tens :
Now draw several rectangles marking each part separately in order to separate the tens :
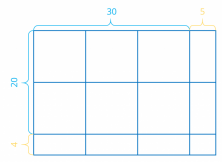
Apply the distributive property of multiplication.
Following the colors used on the graph, the tens colored blue and the ones yellow, when you multiply tens by ones, you can color them green (the color you get when you mix blue and yellow):
24 x 35 = (20 + 4) x (30 + 5) = 20 x 30 + 20 x 5 + 4 x 30 + 4 x 5
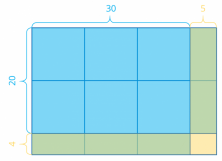
Now, remove the separations between the tens and take note of the multiplication problems represented in each rectangle:
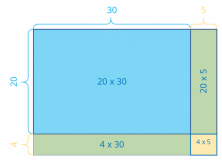
The blue rectangle has an area of 20 x 30 = 600.
The first green rectangle has an area of 20 x 5 = 100.
The second green rectangle has an area of 4 x 30 = 120.
And the yellow rectangle has an area of 4 x 5 = 20.
You can write each result in the corresponding rectangle, like this: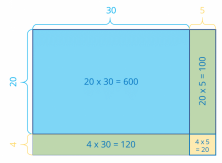 You just have to add the results!
You just have to add the results!
24 x 35 = 600 + 100 + 120 + 20 = 840.
Which can also be written as 24 x 35 = 840.
Understanding the multiplication algorithm with the area model
Now we are going to analyze the multiplication algorithm comparing each step with those of the area model.
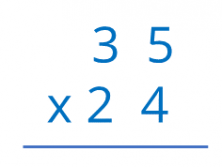
- Begin by multiplying 4 by 35.
First, multiply 4 x 5 = 20 units. Place 0 in the result and carry the 2 to the tens.
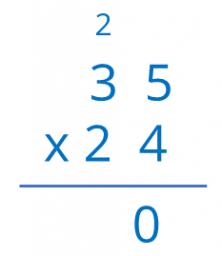
Multiplying 4 units by 3 tens gives us 12 tens, added to the 2 you have, results in 14 tens.
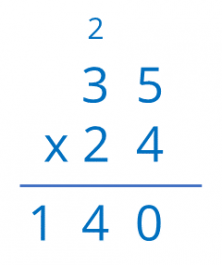
In other words, 140 units, which corresponds with the sum of the areas of the rectangles below (120 + 20).
- Now, multiplying 2 tens by 35 is left.
First, multiply 2 tens by 5 ones, that gives 10 tens as a result, in other words, 100 units, Place the two zeros in the result and carry the 1.
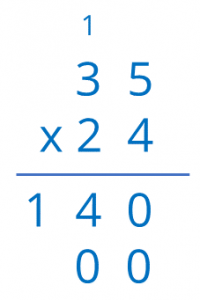
Now, multiplying 2 tens by 3 tens gives us 6 hundreds, added to what you have carried, we get 7 hundreds as a result.
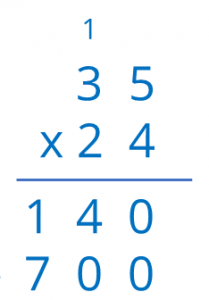
In other words, 700 units, which corresponds to the sum of the areas of the rectangles above (600 + 100).
Now by adding both amounts you get, 140 + 700 = 840, the same result which you got before!
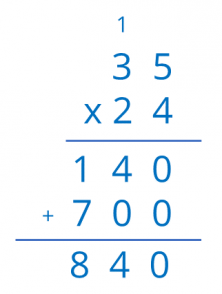
I hope that this explanation has helped you understand the multiplication algorithm better so that you can try it with other multiplication problems. Don’t forget to share this post if you enjoyed it.
And if you want to continue learning more mathematics, log on to Smartick and try it for free!
Learn More:
- Learn Multiplication Algorithm Using Blocks
- Learn about the Distributive Property of Multiplication
- Distributive Property in Geometry
- Notable Identities (Equalities or Notable Products)
- Different Methods of Multiplication







