In this post, you’ll learn another simpler, quicker and more efficient way to multiply these kinds of problems by applying the distributive property in multiplication.
Surely, you all know how to calculate this multiplication problem, 23 x 4, using the multiplication algorithm:
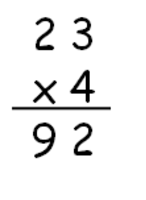
Or maybe you know how to do it mentally. 23 times 4 is “3 times 4 is 12, I bring one up, 2 times 4 is 8, plus the one that I brought up is 9.” 23 times 4 is 92!
The distributive property lets you multiply a sum by multiplying each addend separately and then add the products.
First, we must know how to work smoothly with numbers. For example, if we’re given the number 19, we’ll need to know that it’s the same as 20 – 1, 15 + 4, 10 + 9, etc.
Knowing how to break down a number by adding or subtracting simpler, smaller numbers is going to be very helpful. Let me show you some examples:
12 = 10 + 2 18 = 20 – 2
23 = 20 + 3 39 = 40 – 1
54 = 50 + 4 98 = 100 – 2
110 = 100 + 10 27 = 30 – 3
How can we break down the number that we had in our example before, 23? One of the ways would be by writing it like 20 + 3.
Now we can write the multiplication that we had, 23 x 4, as (20 + 3) x 4, substituting the 23 with 20 + 3. Are you following me? Now, we can apply the distributive property.

Do you guys remember the answer that we got before when we calculated it in a different way? It gave us the same answer, right? 92. We’re going to see this process of using the distributive property with some visuals.
Here are some bars that we’ll use to represent numbers:
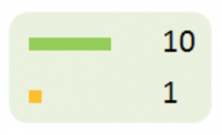
The long bar will represent the 10s and the short one will represent the 1s.
For example, we can represent the number 21 in the following way: We can use the two long bars for two 10s and a short one for the 1.
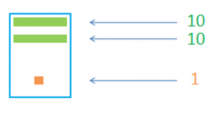
Now, we’re going to see what we can do with 23, going back to our example. We just need to add two more 1s, or in other words, 2 more short bars and we have 23.

Now we know how to represent numbers with the bars. Let’s continue onwards to see how we can represent the multiplication problem.
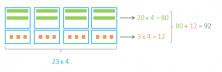
How many times do we need to multiply 23? 4 times because we want to calculate 23 x 4. To do so, we need to draw the 23 four times.
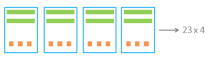
We’ll separate the 23 into 20 + 3.

And the two numbers by 4 separately.
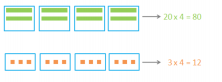
And now, the only thing that’s left to do is add the two numbers.
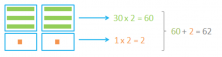
Here’s another example: 31 x 2. Let’s break down the 31 as 30 +1. Then, we multiply the two numbers by 2 and after, we add the numbers together. 31 x 2 = (30 + 1) x 2 = 30 x 2 + 1 x 2 = 60 + 2 = 62.
I’ll give you guys another one:
- 103 x 50 = (100 + 3) x 50 = 100 x 50 + 3 x 50 = 5000 + 150 = 5150
Do you see that it’s easier to multiply 100 x 50 and 3 x 50 separately and later add them than to multiply 103 x 5 directly? We’re going to practice with more examples.
- 99 x 20 = (100 – 1) x 20 = 100 x 20 – 1 x 20 = 2000 – 20 = 2180
- 58 x 4 = (60 – 2) x 4 = 60 x 4 – 2 x 4 = 240 – 8 = 232
- 511 x 3 = (500 + 11) x 3 = 500 x 3 + 11 x 3 = 1500 + 33 = 1533
- 290 x 5 = (300 – 10) x 5 = 300 x5 – 10 x 5 = 1500 – 50 = 1450
I’ll leave you with some more so that you can practice by yourselves:
- 18 x 5 = ?
- 44 x 5 = ?
- 503 x 8 = ?
- 890 x 5 = ?

I hope that from now on, you can use the distributive property to solve these kinds of multiplication problems.
If you liked this post, share it with your friends so that they can learn how to use the distributive property, too!
If you want to keep on learning math, make an account at Smartick and try it for free.
Learn More:
- The Distributive Property of Multiplication
- Distributive Property of Multiplication with Examples
- Learn the Different Properties of Multiplication
- Distributive Property in Geometry
- Learn about the Distributive Property of Multiplication







