In today’s post we’re going to look at the concept of equations. To start, we’re going to take a look at this situation:
“One third of Cecilia’s flowerpots contain daisies, half of them are full of pansies, and the other twelve contain poppies. How many flowerpots does Cecilia have?”
Think about it, and see if you can work it out… No? Well I’ll tell you:
Cecilia has 72 flowerpots.
Now I’m going to explain how I did it. In order to solve the problem, I converted the word problem into a mathematical expression.
“One third of Cecilia’s flowerpots contain daisies […]”

The “x” represents the total number of flowerpots that Cecilia has.
“One third of Cecilia’s flowerpots contain daisies, half of them are full of pansies […]”
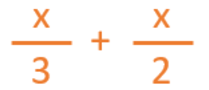
“One third of Cecilia’s flowerpots contain daisies, half of them are full of pansies and the other twelve contain poppies.”
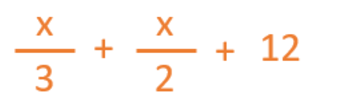
This mathematical expression is equal to the total number of flowerpots that Cecilia has.
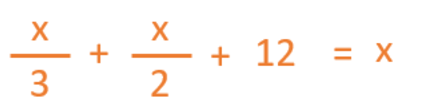
This type of mathematical expression is called an equation. An equation is an expression in which numbers and letters (called variables) related by mathematical operations.
For a mathematical expression to be considered an equation, it must meet the following conditions:
- It must be equal
- It must contain one or more variables (letters)
- The expression can only be solved using the exact values of its variables
Now let’s solve our equation.
The first thing we have to do is find a common denominator for all the elements of the fraction. (You can remind yourself how to add fractions with a different denominator in this previous blog entry).
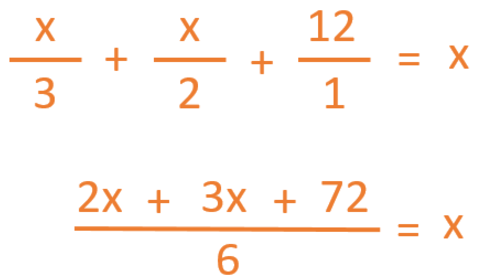
Now we need to move the denominator (6) to the other side of the equals sign. To do this, we change its function. Instead of dividing on the left side, it is now multiplying on the right side.

Now we’re going to put all the variables on the same side of the equation, and everything that isn’t a variable on the other side. To do this, we move the 2x and 3x to the opposite side, and of course, we change the sign.
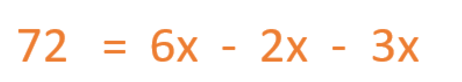
After we solve the operations involving the variables, we are left with the final result.
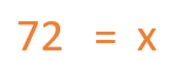
Now you see that Cecilia has 72 flowerpots.
If you want to practise more equations, among many other things, go to Smartick and register for our online method.
Learn More:
- Algebra Problems: 3 Types of Activities in Smartick
- Algebraic Expressions: What Are They? What Are They Used For?
- Reducible Equations: What Are They? How Do We Solve Them?
- Grade 5 Math Word Problems with Smartick
- Powers in Math








Smartick is the best of all learners should learn.