Very often we find, both in mathematical problems and in real life, fraction phrases like: a half, a third or a quarter.
They are the most famous fractions! I’m sure you’ve seen them before.
If you want to see what they are and how to calculate them, you can check out this link:
And if you want more practice with fractions, continue reading and solve some fraction problems with us. Are you ready? Let’s go!
Fraction Problems nº 1:
At the farmer’s market a pound of lemons costs $4, how much does half a pound cost?
It’s a good idea to start by remembering that a single unit is the same as two halves or three thirds or four fourths.
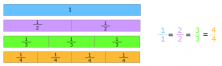
In this case, we have to find the price of a half-pound. We can see that a single unit is equivalent to two halves. So, in order to find out how much half of a pound costs, we have to divide by two and take one of these parts.

The price of a one whole pound is $4, so we divide: 4 / 2 = 2. Half of a pound costs $2
It can also be expressed as follows:
![]()
And…How much would two quarters of a pound cost?
Here, we divide the single unit into four parts and take two parts.

If we think about it, we can see that two quarters is equivalent to a half.

So, two quarters of a pound would cost $2 as well.
It can also be expressed as such:
![]()
Fraction Problems nº 2:
Mark bought three quarters of a pound of lemons. How much did he pay?
He bought three quarters of a pound, so we divide the unit into four parts and take three of them.

Each pound is $4, so we divide 4 / 4 = 1 and multiply by 3. 1 x 3 = 3. He paid $3.
When he got home, Mark squeezed the lemons and got a quarter-gallon of lemon juice. After, he added a half-gallon of water to make lemonade. How much lemonade did he make?
Let’s draw it out:
– He squeezed out a quarter-gallon of lemon juice
![]()
– He added a half-gallon of water
![]()
In order to add a quarter to a half, we have to find the common denominator.
We should already know that two quarters are equal to one half!

So, we add one quarter to two quarters..

And we get three quarters.
![]()
That means that Mark made three quarters of a gallon of lemonade.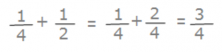
Fraction Problems nº 3:
Peter served 7 glasses of lemonade and 14 glasses of water because some of his friends didn’t like lemonade. What fraction of the glasses that he served had lemonade?

How many glasses did he serve in total? 21! This will be the denominator of the fraction.
How many glasses of lemonade did he serve? 7! This will be the numerator.

But, it can be simplified!
Let’s look at it this way:

How many groups of glasses are there in total? 3
How many of these groups have lemonade? 1
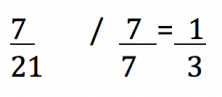
Therefore, the reduced fraction that represents the amount of glasses of lemonade served is one third.
The next time you make lemonade or any other kind of recipe at home, take a look at the quantities! Try to find the fraction and if you discover any tell us by leaving us a comment!
Also, remember that you can log onto Smartick and try it for free if you want to learn more math!
Learn More:
- What do people mean by “a Quarter”?
- Half, Third, Fourth, Fifth in Math: Definition & Calculation
- Learn about Equivalent Fractions and Practice!
- Learn about Fractions: Halves, Thirds and Fourths
- Using Singapore Bars to Help Solve Problems II








I like this page
Thanks 🙂
Greatly simplified!