In today’s post, we’re going to look at an example of how to add fractions. Fractions might seem boring, but, just like anything mathematical, once you understand them they become easy and fun!
To help us explain adding fractions, we’re going to use a resource that we’ve recently developed for the Smartick platform. We think you’ll find it’ll really help you understand these types of operations.
We have to add 1/2 + 1/3. To do this, we need to divide the rectangles into the same number of parts:
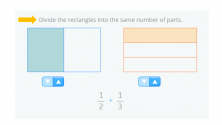
The first rectangle shows the first fraction: 1/2 (the rectangle is divided into 2 parts and 1 is blue).
The second rectangle shows the second fraction: 1/3 (the rectangle is divided into 3 parts and 1 is orange).
We divide the rectangle on the left to make 3 equal rows, the same number of rows as on the right:
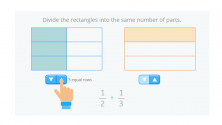
And now we need to do the same to the other rectangle. We divide the second rectangle to make 2 equal columns so that both rectangles have the same number of columns.
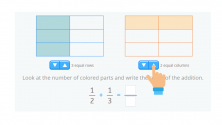Now we just have to add:
To work out the numerator of two added fractions, we need to look at the colored part of the two rectangles. To work out the denominator, we need to count the number of parts each rectangle is divided into.
Therefore, the result of the sum of these fractions is 5/6:
It’s not so complicated when you add fractions this way, is it?
If you liked our article about adding fractions and want to continue practicing, log in to Smartick and try it free. You can have fun working on exercises like this in your 15-minute daily session.
Learn More:
- Adding and Subtracting Fractions: Why Do They Need the Same Denominator?
- Understand What a Fraction Is and When It Is Used
- Homogeneous and Heterogeneous Fractions
- How to Add 3 Fractions with Different Denominators
- Understanding Fractions: “If the Whole Is Made of 8 Parts, How Can I Have 11?”
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.