Do you know what direct proportionality is? What are proportional magnitudes?
If you do not already know, in the previous post on our blog, we explain what direct proportionality is and what we can use it for.
If you already know that, I challenge you to identify which of these three situations is a direct proportionality problem:
- 12 cans of soda cost 60 coins. How much would 10 cans cost?
- On a team of 15 players, there are 8 who bat left-handed and 0 switch-hitters. How many bat right-handed?
- 18 students can be divided into 6 groups of 3 students each or 2 groups of ____ students each.
Have you thought this through?
I bet you have it!
The correct answer is:
12 cans of soda cost 60 coins. How much do 10 cost?
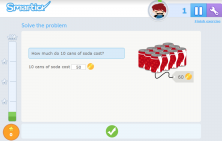
Why?
Because it is the only case in which if one of the magnitudes (the number of cans) increases or decreases, the other magnitude (price) increases or decreases in the same proportion. That is, if we divide or multiply the number of cans by a number, the price will be divided or multiplied by that same number.
In this situation, the number of cans and price are directly proportional magnitudes.
How can these problems be solved?
To solve proportional magnitudes problems, the method of unit reduction can be very useful.
Unit Reduction method
As its name implies, it is about finding what the value of one of the magnitudes is when the other is 1, the unit value.
In this situation the magnitudes are:
- Number of cans (magnitude A)
- Price (magnitude B)
To reduce the unit, we just have to ask:
How much would 1 can cost?
To find out, we divide the price of 12 cans (60 coins) by 12
60 / 12 = 5
Each can costs 5 coins.
We have reduced the unit!
Now we can calculate how much any amount of soda cans would cost … 15, 20, or even 1,000 cans.
We just need to multiply the price of 1 can (5 coins) by the number of cans.
In this case, we ask for the price of 10 cans,
so we multiply 5 × 10:
5 x 10 = 50
We already have the answer! 10 soda cans cost 50 coins!
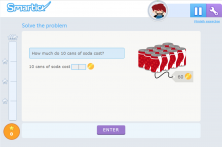
We have solved the problem with the unit reduction method!
Do you know another way to solve it?
There is another well-known way. It begins with the letter “R …”
Do you already know what it is?
If you’ve already found it, be the first to comment in the comment section! If you do not already know, we explain what the rule of three is here.
But if you prefer to keep practicing, go to Smartick and register.
Learn More:
- Inverse Proportionality: What Is It?
- Direct Proportions: What Are They? What Are They Used For?
- Compound Rule of 3: When to Use It and Some Problems
- Inverse Proportionality: The Rule of Three Inverse
- Direct and Inverse Proportionality Problems







