A few months ago we talked in this post about the differences between the Dutch Rekenrek abacus versus the traditional Japanese Soroban and the analogy with hands. Today we will make some comments on the advantages of the Rekenrek compared to the Soroban to encourage varied strategies in children when doing the same calculation.
One of the differences between the use of the Soroban and the Rekenrek is that when using the Soroban, each operation can only be done in a single way. Whereas with the Rekenrek students are encouraged to use several strategies for the same calculation. To explain this, we begin by explaining how it is added in the Soroban. Suppose we want to add 6. In the Soroban there are three different ways of adding 6 depending on which number we add to get 6. To illustrate the three forms, we will add from 6 to get 6.
We start from position 0 in the Soroban, in which all the beads are far from the horizontal bar that separates the above beads, which are worth 5, from the beads below, which are worth 1. We work on the first rod on the right, the units (the second is the tens, etc.). To add 6, we have to bring the upper and lower beads to the horizontal bar. Adding 6 is adding 5 and 1 (6 = 5 + 1).
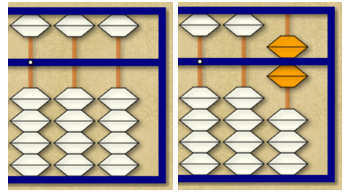
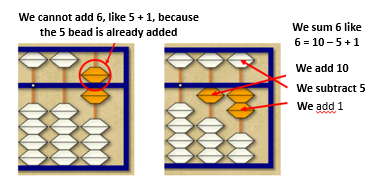
If we want to add another 6, we can not add 5 and 1, since the bead of 5 is already set. We can think of 6 = 10 – 4. Placing 10 is to add a bead in the next rod (of the tens), but to remove 4 since there are no 4 beads, we must remove 5 and place 1. Actually, to add 6 we are doing 6 = 10 – 5 + 1, which in the abacus means adding a bead down on the second rod, removing the top bead from the first rod and adding a lower bead on the first rod.
To add 6 more, there is no problem, since we have the 5 and 1 beads available. The result (of 12 + 6) is 18.
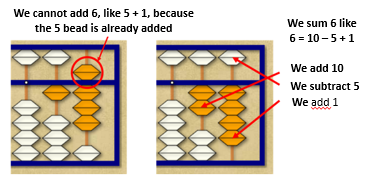
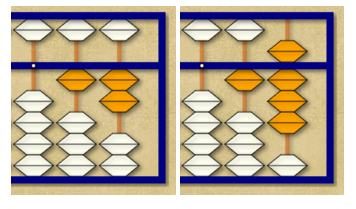 To add 6 more, we must do it as we did in the second step (6 = 10 – 5 + 1).
To add 6 more, we must do it as we did in the second step (6 = 10 – 5 + 1).
Finally, there is a third way of adding 6, which is given in this situation, which is (6 = 10 – 4) and consists of adding 1 ten and removing 4 beads of value 1.
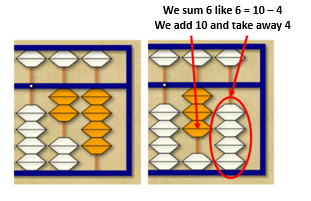
Summing up, each sum can be done in three different ways, depending on the availability of abacus beads. The 6 can be added as 5 + 1, 10 – 4, or 10 – 5 + 1, but whenever we make a concrete calculation (4 + 6) we do the same (4 + 6 = 4 + 10 – 4) adding a bead of 10 and removing 4 beads of 1. This is, therefore, a totally algorithmic process that does not allow variations. There are no different strategies for making a sum. However, in rekenrek, as we will see in the following example, different strategies can be used for the same calculation. For example, to do 7 + 5, you can put 7 in the top row and 5 in the bottom row, and count from 7 until you reach the solution. This is a method of counting from a number that is very important to acquire in the first grade of primary school.
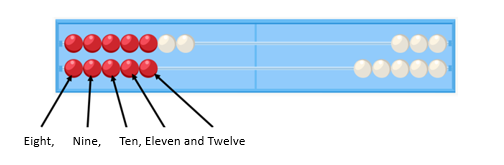
It can also be immediately recognized (subitization) that the top five red and the bottom red are 10 and that, with the 2 white ones, the result is 12. That is, 7 + 5 = 5 + 5 + 2 = 10 + 2 = 12. This strategy is known as the “use of doubles plus two.”

We can remove a bead from above and pass it down, physically or mentally, to recognize that 7 + 5 = 6 + 6 = 12, reducing the calculation again to use of doubles.
 We can also add two white beads down, recognize that we are doing a double, and then compensate by removing the two we have added. 7 + 5 = 7 + 7 – 2. This strategy is called “use of doubles minus 2.”
We can also add two white beads down, recognize that we are doing a double, and then compensate by removing the two we have added. 7 + 5 = 7 + 7 – 2. This strategy is called “use of doubles minus 2.”
 Finally, we can add the missing beads for 10, breaking down the 5 into 3 (what is missing from the 7 to get 10) and 2 (which remains to be added). We call this strategy “step to 10” and it can be represented as 7 + 5 = 7 + (3 + 2) = (7 + 3) + 2 = 10 + 2 = 12.
Finally, we can add the missing beads for 10, breaking down the 5 into 3 (what is missing from the 7 to get 10) and 2 (which remains to be added). We call this strategy “step to 10” and it can be represented as 7 + 5 = 7 + (3 + 2) = (7 + 3) + 2 = 10 + 2 = 12.
 In summary, with the rekenrek, we can do the same operation (7 + 5) in 5 different ways. We believe that it is of great value that children learn to calculate flexibly, that they know several strategies for the same calculation and that they choose the strategy that seems most appropriate in each case. When we speak of mental calculation, we refer not only to calculations made “by head”, or without external aids, instead we speak of a flexible calculation, which enhances the development of the numerical sense, and not a rigid and algorithmic calculation, which can be developed mechanically. That is why, a few months ago at Smartick, we introduced the rekenrek in the sessions for the youngest students.
In summary, with the rekenrek, we can do the same operation (7 + 5) in 5 different ways. We believe that it is of great value that children learn to calculate flexibly, that they know several strategies for the same calculation and that they choose the strategy that seems most appropriate in each case. When we speak of mental calculation, we refer not only to calculations made “by head”, or without external aids, instead we speak of a flexible calculation, which enhances the development of the numerical sense, and not a rigid and algorithmic calculation, which can be developed mechanically. That is why, a few months ago at Smartick, we introduced the rekenrek in the sessions for the youngest students.
Learn More:
- Learn to Add Using the Rekenrek
- Rekenrek Vs. Soroban I: Hand Analogy
- Mental Calculation: Horizontal Addition and Subtraction
- Strategies for Solving Incomplete Horizontal Additions and Subtractions
- Mental Math Strategies for Children







