Have you tried to do our combined operations problems?
When we do a problem, there are times when there is no need to do any operation and other times when you have to do one or many.
Today we are going to see these problems where various operations are necessary in order to arrive at a solution. We call them combined operations problems, and we are going to order them according to the operations that need to be done:
1. Additive Structure Problems
In this type, we include all the problems that involve doing addition, subtraction, or addition and subtraction. For example:
Yesterday, Thomas bought a t-shirt for $15 and a backpack for $23, but they gave him a discount and, in total, he only spent $35. How much of a discount did they give him?
We can solve the problem directly, using the following operation:

They gave him a discount of $3.
Or we can form an intermediary question and answer it first to make it easier for ourselves:
How much would Thomas have paid if he did not get the discount?
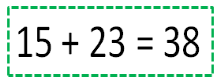
Without the discount, he would have paid $38.

They gave him a discount of $3.
2. Multiplicative Structure Problems
In these types of problems, we include all of the problems that involve doing multiplication, division, or multiplication and division. For example:
At the amusement park, we rode ”The Crazy Wheel,” which is very fun. The security guard told us that the wheel has run 40 times today and it has always been full, carrying 5 children each time. Another attraction, “The Purple Dragon”, has carried 3 times as many children as “The Crazy Wheel.” How many children have ridden on “ The Purple Dragon?”
Let’s do the same as in the previous one.
If we know how to respond to the question directly, we can do the next operation:
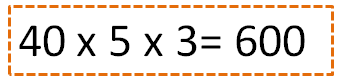
In total, 600 children have ridden.
If not, we came up with an intermediary question to make it easier:
How may children have ridden on “The Crazy Wheel”?
And solve operation by operation:
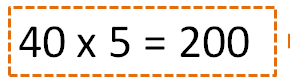
200 children have ridden “The Crazy Wheel.”
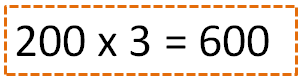
600 children have ridden “The Purple Dragon.”
3. Mixed Structure Problems
In these problems, there is a mix of additive structure operations (addition and/or subtraction) and multiplicative structure operations (multiplication and/or division).
For example, the following problem:

The pirate Silver Beard told me that he has found a treasure on a deserted island that had a total of 3000 gold coins spread equally across three chests. Additionally, in every chest, there were also 200 silver coins and twice as many bronze coins than silver. How many coins were there in total in each chest?
Now it is much more difficult to calculate the solution all at once, right?
For that we are going to come up with and answer the necessary intermediary questions:
How many gold coins were in each chest?
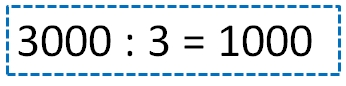
In each chest, there were 1000 gold coins.
How many bronze coins were in each chest?
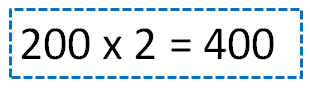
In each chest, there were 400 bronze coins.
Now we are able to answer the last question:
How many coins were there in total in each chest?
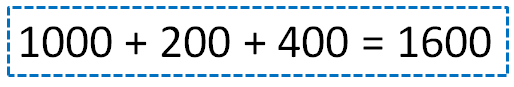
In total, each chest had 1600 coins.
Remember that in order to learn more about combined operations problems and the rest of the primary math problems, you can register now for Smartick free trial.
Learn More:
- Combined Operations: How to Solve These Types of Problems
- What Are Combined Operations?
- How to Solve Combined Operations
- Learn How to Perform Combined Operations
- Using the LCM (Least Common Multiple) to Solve Problems








THIS IS GOOD