In today’s post we’re going to take a look at the compound rule of 3, but first we need to remind ourselves about the simple rule of 3. I’ve selected some previous posts that you can look at if you need to:
As you already know, the simple rule of 3 is related to two proportional magnitudes. The proportionality can be direct or inverse.
The difference between the simple rule of 3 and the compound rule of 3 is that the first relates two magnitudes, and the second relates three or more magnitudes. Although in this post we’re only going to solve problems involving 3 magnitudes, the method of solving problems involving more magnitudes is the same.
Example of the compound rule of 3 involving two direct proportionalities

We are collecting water from the well on my grandparents’ farm. We know that five 2-liter bottles of water weigh 10 kilos. How much do two 3-liter bottles weigh?
The three magnitudes that we have in the problem are: bottles, liters, and kilos. We write out the relation between them knowing that:
5 bottles, 2 liters, 10 kilos
2 bottles, 3 liters, X kilos
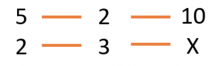
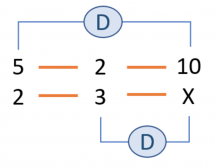
Now we have to work out the relation between the magnitudes, always comparing with the magnitude where the unknown is X.
Comparing bottles with kilos: If there are fewer bottles they will weigh less. There is a direct proportionality.
Comparing liters with kilos: If there are more liters they will weigh more. There is also a direct proportionality.
Now we write the relations in the form of a fraction, in order to be able to find the unknown X. The first fraction includes the unknown (this isn’t obligatory, but it will help solving it later). Next, we represent the multiplication of the two fractions as an equation.
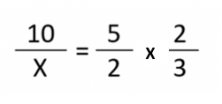
And we solve:
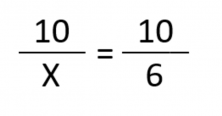
We can find X by using cross multiplication:
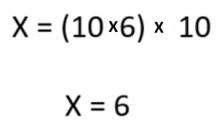
Two 3-liter bottles weigh 6 kilos.
Example of the compound rule of 3 with a direct and an inverse proportionality

6 printers have printed 100 books in 4 days. How many days will it take to print 50 if we have 4 printers?
The magnitudes we have in this problem are: days, printers and books. The relation between them is:
4 days, 6 printers, 100 books.
X days, 4 printers, 50 books.
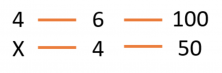
Let’s look at the proportionality between the magnitudes:
If we need to make fewer books, we therefore need fewer days. Direct proportionality.
If there are fewer printers we therefore need more days = Inverse proportionality.
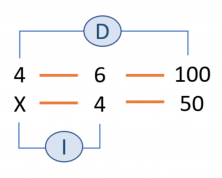
Now we need to write the relations in the form of a fraction, in order to be able to find the unknown X. WATCH OUT! We need to reverse the inverse magnitude, therefore the denominator becomes the numerator and the numerator becomes the denominator.
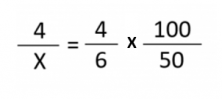
Now we can solve the problem in the same way as the last one, using the cross multiplication method.
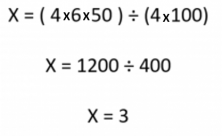
4 printers take 3 days to print 50 books.
I hope you liked today’s post, and have learned how to solve problems using the compound rule of 3.
To keep learning more mathematics, you can register and try Smartick for free!
Learn More:
- Inverse Proportionality: The Rule of Three Inverse
- Inverse Proportionality: What Is It?
- Rule of 3: Direct and Inverse
- Direct and Inverse Rule of 3 Problems
- Direct and Inverse Proportionality Problems








Excellent explanation of such a confusing problem. Kudos to you
Good
The way of explanation is very easy .
Thank you so much for letting me know the compound rule of 3. It confused me before.
Great
Thank you very much. You explained it in an effective way with examples and solutions.
Thanks, explained in a very good manner. Some exercise questions should be added for more practice
Thanks a lot! The explanation is really lucid and in a very easy language.
This website really assisted me in understanding complex proportion more better! I solved all the proportionality problems in my textbook. I really appreciate
The method really made me learn…….