We’re used to working with geometric figures. We find them outlining our notebooks, textbooks, or the screen of our tablets and computers. But today we’re going to look beyond these everyday items and discover the mysteries that some geometric figures hide, and how humans have used or adapted them for their own needs.
In this post we’re going to talk about two geometric figures: the regular pentagon and the triangle.
Regular pentagon
We’ll start with the regular pentagon and an old friend: Pythagoras. He was an Ancient Greek Mathematician and Philosopher. I’m sure you’ve heard of his famous theorem relating to right-angled triangles: The Pythagorean Theorem.
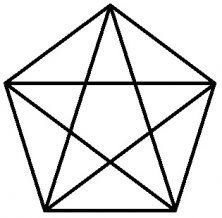
He made many great contributions to philosophy and mathematics, and shared them with the few students at his school. I say few because it was a somewhat elitist school that not everyone could attend. The members of the Pythagorean School were identified by a star pentagon (usually known as a pentagram or pentacle) which is formed by joining the non-consecutive vertices of a regular pentagon.
Triangle
The second geometric figure we’ll be looking at in today’s post, the triangle, offers up a interesting anecdote. It’s protagonist is one Thales of Miletus, another ancient mathematician who discovered 5 very important theorems for projective geometry.
The first of these theorems states that “if a line is drawn within a triangle parallel to any of its sides, a triangle is obtained that is similar to the given triangle”. Using this theorem, he managed to calculate the height of the unexplorable pyramid of Cheops built by the ancient Egyptians. Using this premise, we can establish the relationship of proportionality that exists between the sides of two similar triangles. This was the key to Thales’s calculations.
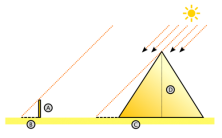
Thales measured the length of the pyramid’s base and the height of his pole. Then, at the same time of the day, he measured the length of the pyramid’s shadow and the length of the pole’s shadow. He knew that the ratio between this distance and the height of the pyramid should be the same as that between the stick and its shadow:
![]() Where he already knew A, B and C.
Where he already knew A, B and C.
Do you want to try it for yourself? Find a building in your neighborhood, or a tree in a nearby park, and calculate its height. You’ll realize how useful geometry can be, lifting us up to the top of the highest towers without moving from the ground.
And if you want to learn more about the secrets that geometric figures hide, here are some questions that have entertained many mathematicians throughout history:
- Why do honeycombs take the form of a regular hexagon?
- Which geometric figure has the largest surface area with the smallest perimeter?
- How can we draw right-angled triangles without using a rule, set square, or any tool that allows us to trace a right angle?
Learn More:
- Pythagorean Theorem: Definition, Proofs and an Example of Practical Application
- How to Calculate Perimeters: Part 1
- Perimeter: What Is It and How to Find It for Any Polygon
- Geometric Shapes with Examples
- Geometric Figures and Straight Lines