How strange is the wording of these problems!
The justification of these convoluted statements that seem like a bad idea by the author.
It has always been so, that when we teach mathematics there are two large areas: that of “exercises” and that of “problems“.
Exercises could be defined as activities to practice how tools are used to solve problems. Thus, the latter would be defined as the example of real situations in which the “mathematical tools” we have learned to use with exercises should be applied.
Just as there are different situations in which we use a nail: to hang a picture on a wall, to join two planks together to make a good shelf … There are also multiple situations in which we use addition, subtraction, multiplication, division, etc.
Thus, in addition to teaching us to use these tools, we must expose our students to the various situations in which we will use them. We achieve this through the use of different semantic categories (in addition to contexts).

This is necessary to teach because, although the operation of resolution is the same, the mental reflection by which the solution is reached, is not the same. The process and sequence of thoughts that lead us to the resolution are not the same and, since what we want is to teach you to solve problems, not to add, we must show the diversity of problems that we can find.
Let’s look at some problems:
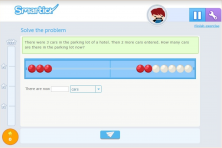
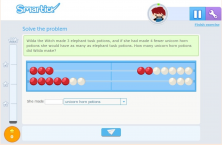
Both problems are solved by an addition, but the thought process, which can be represented by the manipulative material accompanying the problem (Rekenrek), is different.
In the first example, we first represent the initial amount, then add 4 beads, which would simulate the input of the 4 cars, and finally count the number of beads we have.
However, the second problem requires a completely different representation, since the mental process that leads to the solution is much more complex. It requires representation of the number of potions of frog legs and that of the number of potions of unicorn tears, which is represented by the replication of the number of potions of frog legs and the addition of the number of potions less than unicorn tears he should have done so there were as many as potions of frog legs.
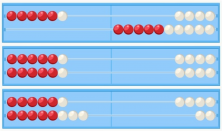
Therefore, although the resolution of addition is taught within kindergarten and the last courses of primary school, addition problems can be learned for much longer, since they are linked with the development of complex logical reasoning which is slowly acquired.
If you want to be able to solve problems like these, register at Smartick and try it for free.
Learn More:
- Modeling Problems With Cubes
- Multiplication Activities in Smartick
- Practice Length Measurement Problems
- Learn to Add Using the Rekenrek
- How to Solve a Multiplication Problem







