In today’s post, we are going to solve a probability problem that appeared in Madrid’s 2008 Standardized Elementary Testing Exam (CDI):

Let’s start by reviewing some probability concepts.
Sample space:
The sample space refers to all of the possible outcomes of a random experiment and it’s often represented by E (or as omega, Ω, from the Greek alphabet).
For example, when we toss a coin, what are all of the possible outcomes that we can end up with? Heads or tails, right? In total, there are two possible outcomes so the sample space is 2.
E = {heads, tails}
And if we throw a die, we have a total of six possible outcomes. The sample space, then, would be 6.
E = {1, 2, 3, 4, 5, 6}.
Event:
An event is any subset of the sample space. For example, coin landings on heads, or a die landing on a 5 are events.
Let’s take a look at what the sample space would be in the first part of our problem.
What are all of the possible outcomes? We’re talking about the number of balls, which are the numbers 11 to 20.
Our sample space is 10:
E = {11, 12, 13, 14, 15, 16, 17, 18, 19, 20}
And the event, which is what we are solving for, is “picking a prime number”.
So then, how do we calculate the probability of this event happening?
When all of the simple events have the same probability of occurring, the probability of whichever event, A, is defined as the quotient between the number of favorable outcomes and the number of possible outcomes. This is Laplace’s Rule of Succession.

In coin tossing example, the simple outcomes would be: heads or tails. If it isn’t a trick coin, the probability of each simple outcome is the same. This means that the probability of the coin landing on heads would be ½.
Going back to our problem: In a bag, there are 10 red and green balls that are numbered from 11 to 20.
Part a): If we pick out a ball without looking in the bag, what is the probability of picking out a prime number?
Let’s start by calculating the number of favorable outcomes and the number of possible outcomes.
Number of favorable outcomes= number of prime numbers = 4 numbers of the possible outcomes are prime numbers (the numbers 11, 13, 17 y 19 are prime)
Number of possible outcomes = 10 (all the numbers from 11 to 20)
The probability of picking out a prime number from the 10 balls is 4/10, which can be simplified to 2/5.
Final answer: P(prime number)=2/5
Part b): How many balls of each color are there?
We’re told that the probability of picking out a green ball is 3/5.
The number of balls that can be picked out, is still 10.
The number of favorable outcomes, or the number of green balls (our event) is one of the questions that we want to solve. We know that 3/5 is equal to 6/10, so if we apply Laplace’s rule:
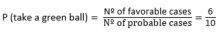
In total, there are 6 green balls in the bag. From there, we can deduce that what’s left, 4 are red balls.
Final answer: There are 6 green balls and 4 red balls.
If you thought this post was interesting and if you’d like to keep on learning Math, Smartick has even more problems that are perfect for practicing!
Learn More:
- Probability: What It Is and How to Calculate It with Examples
- Learn How to Factor into Prime Numbers
- Some Prime Number Curiosities
- Learn and Practice How to Use Exponents in a Word Problem
- Multiplication of Decimals Using Money








Cool
I love it