In earlier posts, we have learned what a percent is and how to calculate it.
Today we are going to use the rule of three to solve different types of problems related to percentages.
Rule of three to calculate the percentage of a number
For example, we want to calculate 30% of 360.
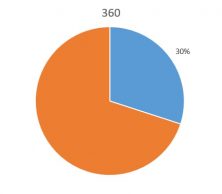
30% means 30 for each 100. So the approach would be: if I have 30 from 100, I have X from 360:
100 —— 30
360 —— X
X = (30 x 360) / 100
X = 108
So, 30% of 360 is 108.
Rule of three to calculate a quantity knowing the percentage of it
For example, we know that 25% of a quantity is 49. What is the quantity?
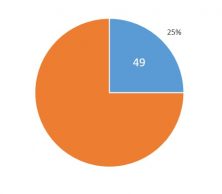
If 25% is 49 then the 100%, which we do not know, will be X :
25 —— 49
100 —— X
X = (49 x 100) / 25
X = 196
The quantity we are looking for is 196.
Rule of three to calculate the percentage represented as a quantity of another
What percentage of 250 does 50 represent?
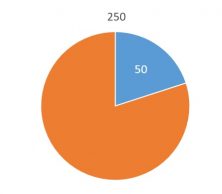
250 is the 100% and 50 is the percentage that we do not know, X :
250 —— 100
50 —— X
X = (100 x 50) / 250
X = 20
50 is 20% of 250.
Rule of three to calculate the percentage of an unknown quantity knowing another percentage of the quantity
We know that 40% of a quantity is 78, how much would 60% be of the same quantity?
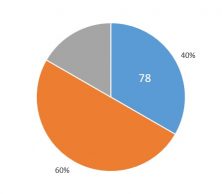
The 40% is 78 and we want to calculate 60%, which will be X :
40 —— 78
60 —— X
X = (78 x 60) / 40
X = 117
So 60% of this quantity is 117.
Today we have learned to solve different problems related to percentages using the same tool: the rule of three. To learn more about this and other contents from primary mathematics, check out Smartick and try it for free.
Learn More:
- Learn the Basic Concepts of the Rule of 3
- Percentage: What Is It and How do We Calculate It?
- Direct and Inverse Rule of 3 Problems
- Singapore Bar Model and Percentages
- How to Calculate the Least Common Multiple Using a 100 Square
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.