In this post, we are going to look at the concepts of ratio and proportion using an everyday element: a photograph.
Have you ever looked at yourself in a photo and thought you looked a little different after changing its size?

Taller, with a longer face, or maybe shorter…
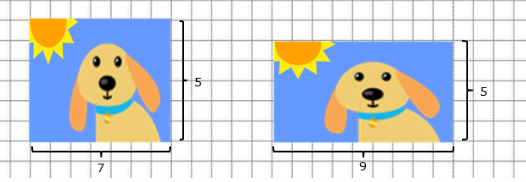
You’ve got to pay attention to proportion!
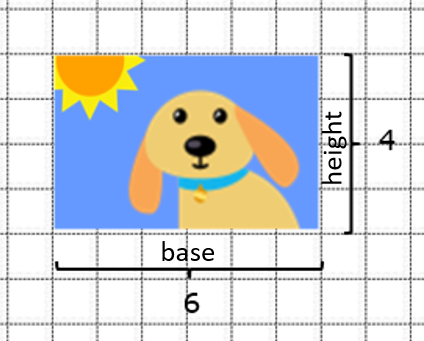
When we take a photo, the photo has a base and height.
For example: Here, we have our original photo that has a base of 6 cm and a height of 4 cm.
If we want to change its size without changing the photo, we need to make sure that the ratio between the base and the height of the photo stays the same.
But…
What is the ratio? How can we figure out the ratio between the base and height of this photo?
- A ratio is a comparison between two magnitudes that can be carried out through a quotient.
- It’s usually expressed as a fraction, or by placing a colon (:) between the two magnitudes.
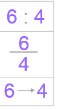
In this example, the ratio between the photo’s base and height is 6:4. If we divide 6 by 4, we get the answer 1.5. This means that the base of the photograph is 1.5 times bigger than its height. Or in other words, it means that for every cm that the photo measures in height, it measures 1.5 cm in width.
Now that we know what the ratio between the photo’s base and height is…
How can we calculate the photo’s new dimensions without deforming it?
There are two ways to go about it:
- Finding the equivalent ratio:
Multiplying or dividing both magnitudes by the same number. For example, we can multiply the base and height by 2.
6 x 2 = 12 and 4 x 2 = 8
Then, the new base would be 12 and the new height would be 8.
- Finding the proportionality constant:
The proportionality constant is the quotient of the ratios of a proportion. In our example, it would be the answer to dividing 6 by 4.
6 ÷ 4 = 1.5
Keeping this in mind, if we want the height of our photograph to be 6 cm, we only need to multiply 6 by 1.5 in order to know how long the base should be.
6 x 1.5 = 9
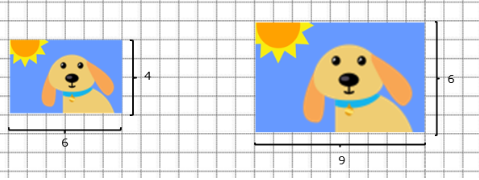
By using any of the two methods, we can make the size of the photograph bigger without modifying its aspect.
It stays the same because we have conserved the proportion!
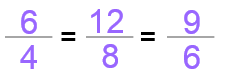
Now we know what those editing programs on our computers automatically do when we click on the “maintain or block aspect ratio.”
Was this post helpful for you? Do you understand what ratio and proportion are?
Make an account now at Smartick and you’ll learn plenty more about ratio, proportion and elementary math.
Learn More:
- Proportional Numbers Problems. Ratio and Proportion
- Proportional Relationship and Examples in Everyday Life
- Direct Proportions: What Are They? What Are They Used For?
- Difference between Mathematical Constants and Variables
- Direct and Inverse Proportionality Problems








I think this website is a really good website to learn about math and the different types it has to offer to the students.