In today’s post, we’re going to study the concept of ratios using the “Singapore Bar Model” methodology.
First, we need to take into consideration that two quantities can be compared in different ways. By subtracting, by a fraction, and by multiplying…but today, we’re going to use ratios as a factor of comparison.
To be able to compare two or more quantities by using ratios, they need to be expressed in the same unit. Once we have the quantities expressed in the same unit, we need to find one of the quantities with respect to the other.
Let’s look at an example:
“John and Paul are twin brothers. Their mom bought them a bag of muffins that has 4 identical muffins. What is the muffin ratio for the brothers?”
The muffin ratio in respect to the number of boys is 2 muffins for each boy and it’s written as (2:1). The relationship is bidirectional, it can also be (1:2), which means that there is one boy for every 2 muffins.
Now, we’re going to apply this to the Singapore Bar Models:
What is the ratio of 4 orange units for 8 blue units?
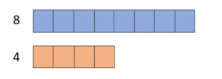
The answer is the same as the one from the previous example.1:2 (there is 1 orange unit for every 2 blue units) and 2:1 (there are 2 blue units for every orange unit)
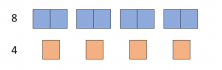
Now, let’s look at a different case where the two quantities aren’t divisible by each other:
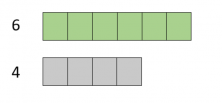
Here, we see a direct relationship; the ratio between these two quantities isn’t divisible by one another. 6:4 (6 green units for every 4 grey units) and 4:6 (4 grey units for every 6 green units).
Now, we’re going to check to see that other unit comparisons can have the same ratio:
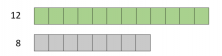
6 green units for 4 grey units and 12 green units for 8 grey units have the same ratio because the relationship between said quantities is the same.
To learn more about this topic, and others, sign onto Smartick and try out our elementary math learning method.
Learn More:
- Proportional Numbers Problems. Ratio and Proportion
- Singapore Bar Models for Multiplication and Division
- Proportional Relationship and Examples in Everyday Life
- Singapore Bar Model and Percentages
- Ratio and Proportion: Concept and Some Examples
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.