In today’s post, we are going to talk about the concepts double and half. First, I will explain what each term means and then we will see a strange situation with them.
Double and half explain a type of relationship that exists between two numbers or quantities.
Double of a quantity
The double of a quantity is the result of adding the same amount to itself. The final quantity is double the initial.
Let’s look at an example.
What happens when we double 3 oranges?
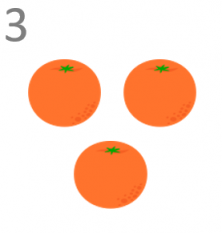
We should add these 3 oranges to another 3 oranges.
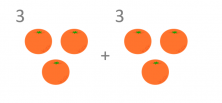
The result of adding the same quantity twice is double that quantity. In other words, doubling 3 oranges is calculated by adding 3 oranges and 3 oranges, which is 6 oranges in total.

Therefore, the double of 3 oranges is 6 oranges.
Half of a quantity
Half of a quantity is the result of dividing the said quantity into two equal parts. Each one of these parts is half of the initial quantity.
Let’s look at an example.
What will be half of 8 tomatoes?

We should divide 8 tomatoes into two equal quantities.

The result of dividing 8 tomatoes into two equal quantities is 4 tomatoes. These two quantities now form the distribution of the 8 tomatoes, they are halves of the original quantity.
Therefore, half of 8 tomatoes is 4 tomatoes
If we look at it we will see that double and half are related and inverse concepts. In other words, a number is the double of another, which means that the latter is ultimately half of the first.
For example:
Two times 5 is 10 and because of this we say that 10 is 5 doubled. If we analyze this relationship in reverse we see that 10 can be divided into two equal parts, and because of this we can say that 5 is half of 10.
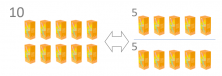
10 milkshakes are 5 milkshakes doubled, just like 5 milkshakes are half of 10 milkshakes.
I hope that this post has helped you to learn the concepts of double and half, and remember if you want to work on these and other interesting mathematical concepts for primary school, check out Smartick and discover our method.
Learn More:
- Learn about Fractions: Halves, Thirds and Fourths
- Adding and Subtracting Fractions: Why Do They Need the Same Denominator?
- Mathematical Functions: Do You Know What They Are?
- Half, Third, Fourth, Fifth in Math: Definition & Calculation
- Proportional Relationship and Examples in Everyday Life







