Aug03

The Distributive Property of Multiplication

Hello! We’re back again. Today we will look at one of the properties of multiplication: the distributive property of multiplication.

As you may know, multiplication has different properties, let’s review them:

Commutative property
Associative property
Identity Property
Distributive property

Let’s focus on the distributive property of multiplication

The distributive property of multiplication states that when a number is multiplied by the sum of two numbers, the first number can be distributed to both of those numbers and multiplied by each of them separately, then adding the two products together for the same result as multiplying the first number by the sum.

Let’s look at the distributive property with this example:

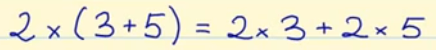
distributive property of multiplication

According to the distributive property 2 × (3 + 5) will be equal to 2 × 3 + 2 × 5

Let’s check to see if this is true.

2 × (3 + 5) = 2 × 8 = 16

2 × 3 + 2 × 5 = 6 + 10 = 16

In both cases we get the same result, 16, and therefore we can show that the distributive property of multiplication is correct.

I hope that this explanation helps you understand this important property of multiplication.

Go and practice! In Smartick we have lots of exercises for you to learn the best math.

Learn More:

Fun is our brain’s favorite way of learning

Diane Ackerman

Smartick is a fun way to learn math

15 fun minutes a day
Adapts to your child’s level
Millions of students since 2009

Author
Recent Posts

Smartick

Content Creation Team.
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.