Jan22

Different Methods of Multiplication

In today’s post we’re going to find out how ancient cultures would have solved the multiplication we’ve chosen.

It will help you to better understand how the classic multiplication algorithm works. I’m sure you’re already an expert in multiplication, but you might not understand exactly why it works the way it does.

We’re going to look at Chinese and Egyptian methods of multiplication. To help make sure you’ve understood, we’ll demonstrate each method by solving the multiplication 31 x 42 using both.

Chinese Method of Multiplication

This Chinese method originally involved using bamboo sticks to help them with multiplication, arranging them horizontally and vertically, as we’ll see in the example.

Let’s find out how to multiply 31 x 42 using this method.

First, place:

3 horizontal lines separated by the same distance, and 1 more horizontal line a bit further apart.
4 vertical lines separated by the same distance, and 2 more vertical lines further apart.

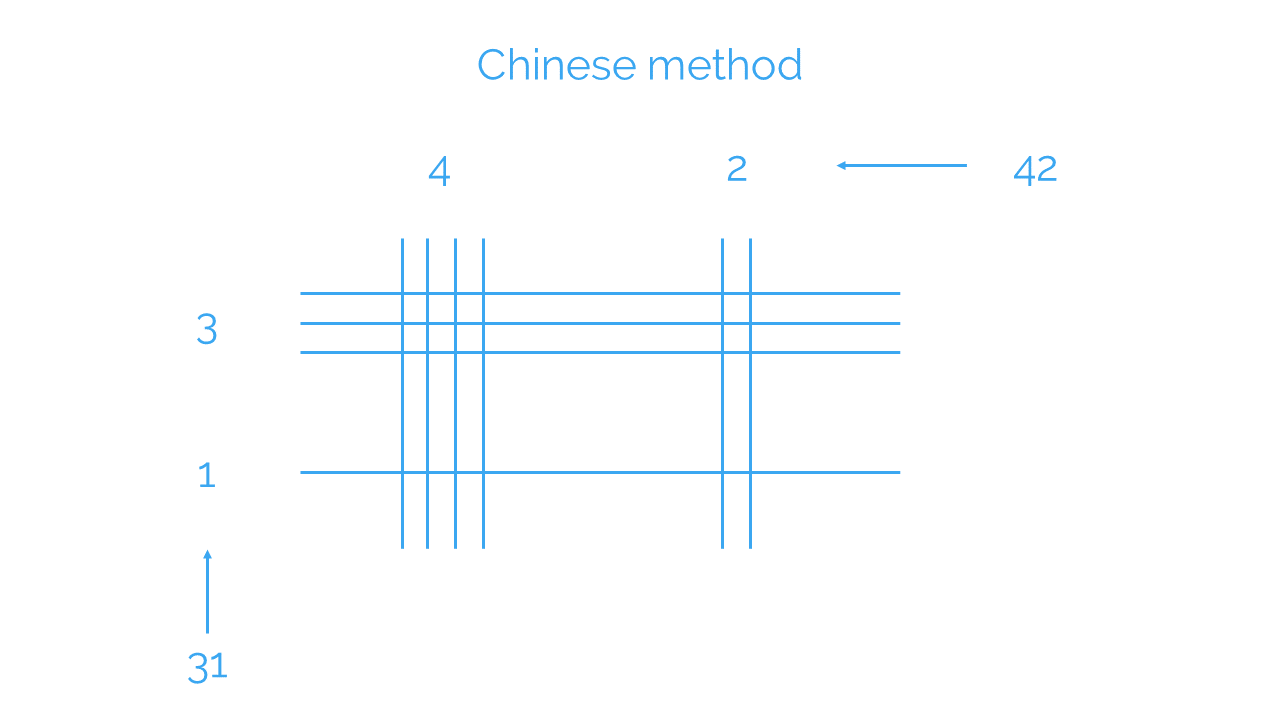Multiplication Next, count the number of times each pair of lines cross. Make sure you keep track of which ones correspond to the tens and which represent units:

Where the unit lines cross, we get the units of the result (since the product of units gives units).
Where the unit lines and tens lines cross, we get the tens of the result (since the product of units and tens gives tens).
Where the tens lines cross, we get the hundreds of the result (since the product of tens gives hundreds).

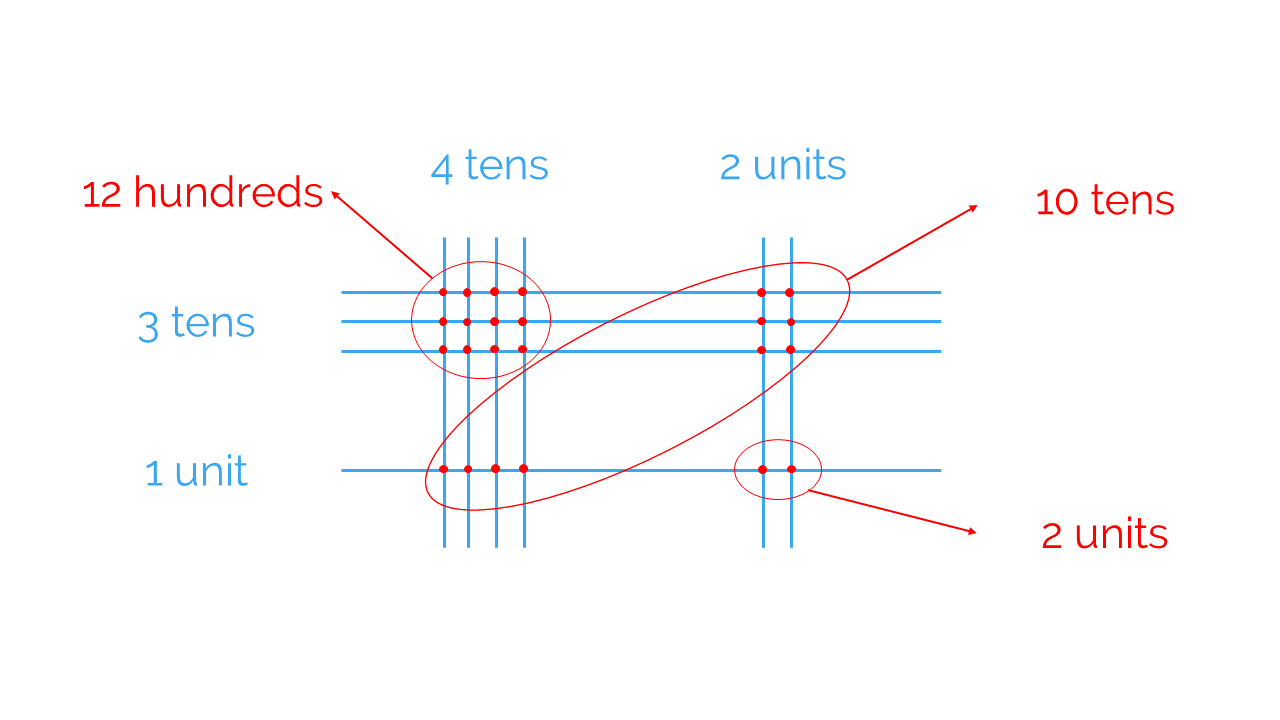Multiplication Now you can arrange all the information you’ve obtained into the result of 31 x 42:

2 units.
10 tens, which is the same as 1 hundred.
12 hundreds, which when added to the hundred given by the 10 tens makes 13 hundred. These 13 hundreds can be written as 1 thousand and 3 hundreds.

So, we’ve got:

1 thousand, 3 hundreds, and 2 units: 1,302

Therefore we know that 31 x 42 = 1,302

Egyptian Method of Multiplication

The ancient Egyptians multiplied using a method that involved breaking down the multiplication into a series of additions, then doubling one of the factors (putting them into powers of 2).

Let’s look at how to multiply 31 x 42 using this method.

First of all, we need to place 1 and 31, and start doubling the two quantities. Like this:

Multiplication

You’ll get different multiplications of 31 by powers of 2, like this:

Multiplicación

Now you need to look for the numbers that help you solve the multiplication 31 x 42. To do this, you just need to find the powers of 2 that add up to 42:

32 + 8 + 2 = 42 Multiplicación At this point, you will have managed to break down 31 x 42 into sums that you can calculate easily:

31 x 42 = 31 x (2 + 8 +32) = 31 x 2 + 31 x 8 + 31 x 32 = 62 + 248 + 992 = 310 + 992 = 1,302

And as you can see, the result we get once again is 31 x 42 = 1,302

I hope these multiplication methods have helped you to better understand how multiplication works. Share them with your friends, so they can become experts in multiplication too!

If you want to keep learning and practicing maths, register with Smartick and try it for free!

Learn More:

Fun is our brain’s favorite way of learning

Diane Ackerman

Smartick is a fun way to learn math

15 fun minutes a day
Adapts to your child’s level
Millions of students since 2009

Author
Recent Posts

Smartick

Content Creation Team.
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.