In today’s post we’re going to learn how to solve algebraic equations using the Singapore bars method.
This method helps us to visualize the information graphically when we read an algebraic word problem, which helps us to solve it.
Let’s look at an example of how to solve an algebraic problem with and without Singapore bars.
Example of an algebraic problem
There are 50 boys and girls at the summer camp this year. If there are 10 more boys than girls, how many girls are there?
First, we’re going to see how to solve it without the help of the Singapore bars. Once we’ve done that, we’ll use the bars to help us and compare the difference between the two methods.
1. Solving algebraic equations without vizualisation
To solve this problem directly, using the algebraic method of resolving equations (without vizualisation) we can use a letter, like x, to represent the number of girls, which is at first an unknown quantity:
x -> number of girls at the camp
Since there are 10 more boys than girls, the number of boys is x + 10:
x + 10 -> number of boys at the camp
So the total number of boys and girls will be x + (x + 10):
x + (x + 10) -> total number of boys and girls at the camp
And since we already know that the number of boys and girls is 50, we can use the following equation to solve the problem:
x + (x + 10) = 50
If we remove the parentheses, we get:
x + x + 10 = 50
We can arrange it like this:
2x + 10 = 50
Subtracting 10 from both sides gives us:
2x = 40
And, finally, if we divide by sides by 2 we get:
x = 20
Therefore, we can see that there are 20 girls at the summer camp this year.
2. Solving algebraic equations with visualization (Singapore bars method)
Using the Singapore bar method we can draw a comparative model to represent the problem, and resolve it using two alternative methods:
- Unitary method
- Algebraic method
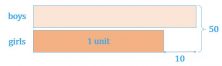
This model shows that the total numbers of boys and girls is 50 and that the difference between the number of boys and girls is 10.
Using this visualization, we’re first going to solve the problem via the unitary method and then via the algebraic method.
-
First method: Unitary
We take the number of girls as 1 unit. We can look for the value of 1 unit and solve the problem like this:
Since 2 units plus 10 equals 50:
We have:
2 units + 10 = 50
If we subtract 10 from both sides we get:
2 units = 40
And finally, if we divide both sides by 2, we are left with:
1 unit = 40 ÷ 2 = 20
Therefore, since one unit represents the number of girls, we can see that there are 20 girls at the summer camp this year.
-
Second method: Algebraic
Like in the very first example, we use the letter x to represent the number of girls.
This model allows us to express the number of children in terms of x, as shown above. There are several variations of this method, so we’ll look at just one of them.
The number of boys is 10 plus the number of girls. This is expressed as x + 10.
The model shows that x + (x + 10) equals 50, giving the equation:
(x + 10) + x = 50
Just as in the previous steps, we get the same solution to the equation: x = 20.
Again, since the letter x represents the number of girls, we can conclude that there are 20 girls at the summer camp this year.
What do you think about this method of visualizing algebraic equations to make it easier to solve? I hope that you’ve found it useful and that you’ll be able to use it when you solve equations in class and everyday life.
And if you want to keep learning and practicing mathematics, go to Smartick and try it for free.
Learn More:
- Singapore Bars Applied to Fractions
- Using Singapore Bars to Help Solve Problems II
- Singapore Method: Using the Singapore Bar Models to Solve Problems
- Singapore Bar Model and Percentages
- Let’s Learn about Ratios with Singaporean Bar Models