Today, we’re going to walk through some examples of adding fractions.
Before you read this post, you might want to check out a previous post where we explain how to add fractions step by step.
Let’s begin with the simplest of examples:
Adding Fractions with the Same Denominator
For example:
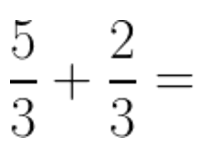
The only thing we need to do is add the numerators and leave the denominator alone. The answer is:
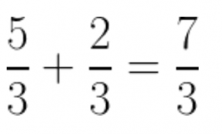
Adding Numbers and a Fraction
For example:
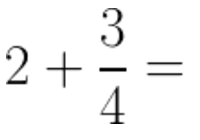
The first thing that we need to do in this case is to convert the 2 into a fraction. As you already know, we can simply put a 1 in the denominator of any number without changing its value:
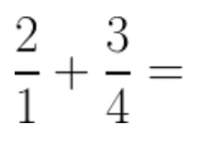
When we have two fractions, we can start looking for the common denominator. In this example, it’s quite simple because the least common multiple of 1 and any number is that number. So:
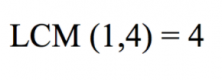
Now, we only need to multiply 2 x 4 and we get:
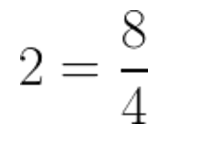
…and now we put it into our addition problem:
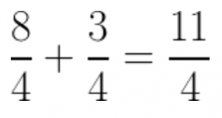
Adding Fractions with Co-Prime Denominators
Remember that two numbers are co-prime if their greatest common divisor is 1. For example, in the problem:
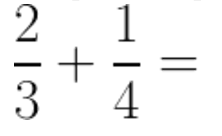
The denominators are co-prime because:
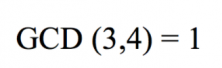
These kinds of problems are simple to solve because the only thing that we need to do to find the new numerators is to multiply each numerator by the denominator of the other fraction, as shown below:
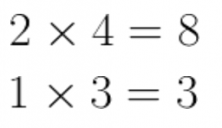
And we simply multiply the denominators together. So, we get:
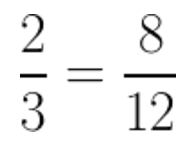
and
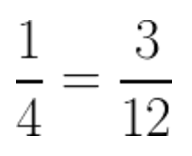
And the only thing that’s left to do is to add the two fractions together:
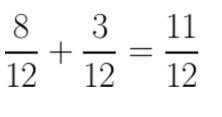
Adding Fractions in General
For example:
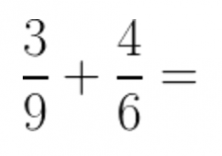
We need to calculate the least common multiple of the denominators:
![]()
What do we have to do next? Let’s break it down. First, let’s look at the fraction:
![]()
To find the numerator, we need to divide the LCM by the fraction’s denominator:
![]()
We need to multiply the fraction’s numerator by 2. So:
![]()
And we can see that the new numerator is 6.
For the denominator, we just need to use the GCM (18):
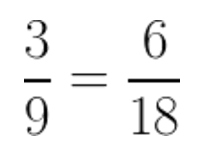
Now, we just do the same thing with the other fraction. To solve for the numerator, we need to divide:
![]()
And multiply by the numerator:
![]()
Then, we put in the GCM as the denominator, which gives us:
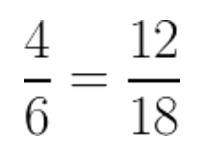
Now, all that’s left to do is to add the fractions together …
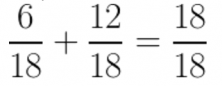
And that’s it!
We actually add all fractions this way, the first examples were simpler thanks to the GCM that was easier to work with. The way of solving the problems, however, always stayed the same.
To summarize, the steps for adding fractions are:
- Find the GCM of the two denominators.
- Divide the GCM by the denominator and multiply that by the numerator to convert each fraction into a fraction that has the GCM as the new denominator.
- When we’ve done the two previous steps with all the fractions, put them all in order and add their numerators.
If you want to continue learning math, register today for Smartick!
Good luck adding fractions—with a little practice, you’ll see that they’re a snap and you’ll get it in no time!
Learn More:
- How to Find a Sum of Fractions
- Learn and Practice How to Subtract or Add Fractions
- Learn and Practice How to Multiply Fractions
- Two Ways of Dividing Fractions and Some Examples
- Learning How to Subtract Fractions








it helps a lot
Adding of fractions
Thanks
Good
I think I get it
I think this will work for me. I need a lot of help with my work.
nice
Lcm
Great
Thank you it’s so helpful
Thanks,,,,it’s so helpful…
thank you! it really helps
Well explained.
It was helpful and very detailed. My son loves this program and he said it’s very easy to understand. Thank you
Thank you Leo Messi 😉
Thanks so much for your help
Well explained, thanks.
Thanks for your easy and simple methods
Thank you very much for this lesson
This helped me and my 10 year old daughter in math. THANK YOU SO MUCH!!!!!!
I am very happy
It help me a lot in teaching Math 4. Thank you.