At Smartick, we support the combination of pedagogical methods and approaches to achieve excellence in the teaching-learning process. However, this does not arise from a mere whim but is based on real experiences of success which prove that the best way forward in the field of education is none other than utilizing the best sources and taking the best of each method and approach.
The Netherlands, an exemplary system in the use of alternative algorithms
The Dutch curriculum is a good example of teaching alternative algorithms in conjunction with traditional ones. These are the steps that must be taken to do so:
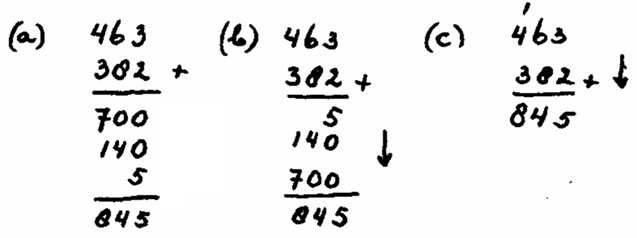
In the image, we see the process of learning the traditional algorithm, starting with the alternative algorithm:
a) The alternative algorithm involves the following steps: 400 and 300 make 700; 60 and 80 make 140; and 3 and 2 make 5. This breakdown process is learned earlier in mental calculation. Then, the partial results are added mentally, by means of a chaining method: 700 and 140 make 840; and 5, 845. As we can see, this algorithm develops from left to right, which is the most “natural” way to add. Its a closed algorithm based on numbers, since 4 and 3 are not added in the hundreds column but 400 and 300.
b) A “transition” algorithm is shown. Its not an algorithm designed to be performed habitually, but instead serves as a “bridge” between the alternative and traditional algorithms. Its only difference to the alternative algorithm is that the operation proceeds from right to left, which is something that should not cause problems since it doesn’t matter which side the operation is started from when there are no “carried” numbers.
c) We see the traditional algorithm, which is a compressed form of the “transition” in which we write the partial sums on one line.
The didactic keys
The didactic keys of this three-step sequence from the alternative to the traditional algorithm are the following:
- Algorithms in The Netherlands are studied later, and much less time is devoted to them. Students have previously studied mental calculation, and the algorithms rely on methods of mental calculation such as breaking down numbers and chaining.
- The alternative algorithm is learned first, because it is the most natural and easiest to understand. It also favors the understanding of positional value, integrates written calculation with mental calculation and estimation, and avoids the difficulty of lack of comprehension of carrying within the sum. From a didactic point of view, it offers great advantages with respect to the traditional algorithm.
- The passage from the alternative to the traditional algorithm is not immediate and requires specific didactic work, which gives rise to a transition algorithm. It contains some characteristics of the alternative algorithm and others of the traditional one (Step B in the previous image). It is, so to speak, in the middle of the two algorithms, and serves as a “bridge” between them.
- Then the traditional algorithm is studied. However, the previous study of the alternative algorithm helps understanding of the traditional algorithm, which is “less didactic”.
- In the end, students learn two algorithms, the alternative and the traditional. Each algorithm facilitates the understanding of different aspects of the decimal numbering system. The alternative algorithm better facilitates the learning of positional value while the traditional algorithm involves the use of carrying numbers.
Therefore, at Smartick we opt to teach addition and subtraction algorithms that combine the use of the traditional algorithm with alternative algorithms as a support tool to facilitate understanding. If you want to find out how we do it, register with Smartick and try it for free.
Learn More:
- Is It Good to ¨Mix¨ Alternative Algorithms, Such as ABN, with Traditional Ones?
- Mental Calculation: Horizontal Addition and Subtraction
- Review Addition Algorithm and Vertical Addition with Carrying
- Subtraction with Borrowing: An Explanation of Two Different Algorithms
- Solve and Analyze Numerical Place Values
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
Thank you for your helpful advice, I have really enjoyed reading and learning about algorithms.