In this post, we’re going to decipher an answer’s sign by looking at the sign of a number’s power.
To start off, let’s look at an example of what happens when the factor’s signs mingle.
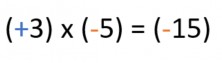
As we already know, we multiply the factors normally and later, we add the appropriate sign to the answer.
Let’s see what happens with a power.
A power is a succession of the same product, as shown in the example below.
So then, if the power has a positive sign and the exponent is even and positive as well, like in the example, the answer will be positive, too.
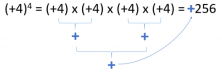
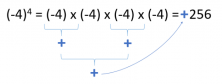
If the even exponent and sign are negative, the answer would also be positive. This happens because each negative sign cancels the other out (- x – = +) and they form a positive answer.
We can also see cases where the exponent is odd and positive. In such cases, we’d get a positive answer yet again.
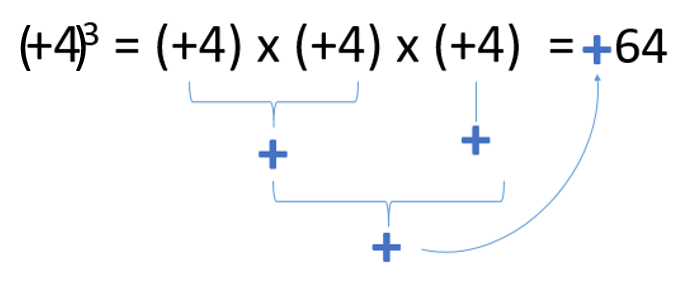
If we take all these situations into account, we could say that the last case, an odd exponent with a negative sign, is the only exception that gives a negative answer.
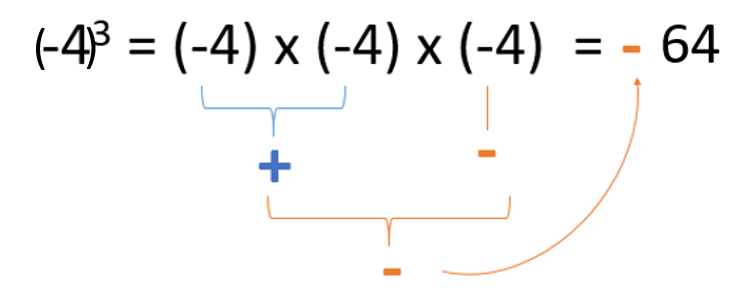
This happens because the odd number of factors means that we have a negative sign that’s left out. So despite all the other pairs having a positive (+) result, the last negative number (-) makes the final answer negative.
I hope that this post helps you quickly determine the signs of all the powers that you encounter in problems.
If you want to learn more about this topic and other math topics, make an account at Smartick and try out our online learning method.
Learn More:
- Learn Everything About the Properties of Powers
- Properties of Powers II
- Learn about the Importance of the Parentheses in Powers
- Do You Want to Learn the Properties of Powers?
- Learn More about Exponents
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.