In today’s post we’re going to continue talking about the properties of powers.
Before we go on, you might find it useful to review the concept of a power, its elements and how to solve them. You can take a look at these previous Smartick blog entries if you need a reminder:
- Powers: What They Are and What They Are For
- Properties of Powers I
Once you’re up to speed with all this information, we can move on.
Powers with a negative integer exponent
This property only applies to a power with a base that is not zero (0). When we find a base that meets this condition with a negative integer component, we can say that this power is equivalent to a fraction with a numerator of 1 and a denominator which is the given power, but with the sign of the exponent changed (from negative to positive). 
Let’s take a look at this property applied to a specific case. Here we can see that 3 to the power of minus 2 is the same as the fraction one over 3 squared: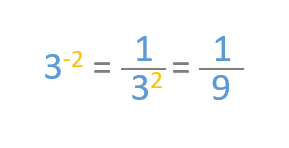
Powers of another power
As you can see here, a power of a power is the same as a power with the same base but with the two exponents multiplied by each other:
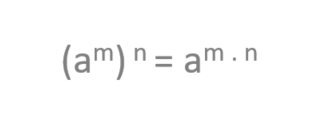
Let’s look at an example. If we raise 3 squared to the power of 3, we get the same result as if we raise 3 to the power of 6. In both cases, the result is 729.
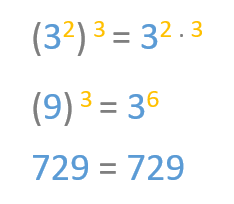
Multiplying powers with the same exponent
Here we see that if we multiply two powers with the same exponent, we get the same product as if we multiply the bases first and then raise the result by the shared exponent.
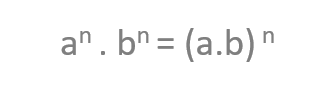
Now let’s look at an example. We can see that multiplying 5 squared by 3 squared gives the same product as multiplying 5 by 3 and raising the result by 2.
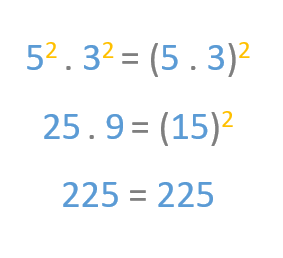
Dividing powers with the same exponent
If we’re faced with a division between two powers with the same exponent, we’ll obtain the same quotient if we divide the bases first before elevating the result of the division by the shared exponent.
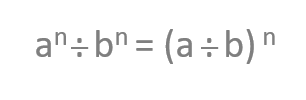
Take a look at this example. We get the same quotient if we divide 6 squared by 2 squared or if we divide 6 by 2 and then raise the result by 2. Take a look:
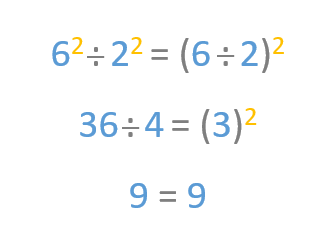
I hope this article has helped you learn the properties of powers!
Remember, if you want to practice primary math exercises, you can find them in our daily sessions. Log in to Smartick and try our online math learning method for free!
Learn More:
- Learn Everything About the Properties of Powers
- Do You Want to Learn the Properties of Powers?
- Powers of Base 10, Base 100 and Numbers Followed by Zeros
- Powers: What They Are and What They Are For
- Learn about the Importance of the Parentheses in Powers
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.