Thanks for choosing Smartick to continue learning math are you ready to begin with square roots? Well, let’s go!
In this week’s post, we will learn to calculate exact square roots and some visual examples where they apply. As you know, graphical visualization is always a great help in understanding and assimilating new concepts. I hope you find it very useful and enjoy learning. You will see how simple this is for the square roots!
To calculate the square root of a number, find the number that, when multiplied by itself, gives us that first number. If we already know the degree 2 powers (calculate the square of a number), we try to find the number that raised to the square gives us the first number.
To represent the square root, the symbol we use is drawn as follows:
Let’s look at some examples of how to calculate exact square roots, which are the roots that give us an exact number (without decimals).
Exact Square Roots
To calculate the square root of 9, you have to find the number that multiplied by itself gives us 9. Let’s think a little to make sure that we know it. Do you already have it? Exactly! As you probably guessed, that number is 3. So the square root of 9 is 3.
If we already know the powers, we can look for the number that, when squared, gives us 9, and as 3 squared is 9, the number that we are looking for is 3.
Have you seen how easy? You can now try to calculate the square root of 16. Have you found it already? That is since 4 squared is 16, the square root of 16 will be 4.
Let us now look at some visual examples to better understand the concept of the square root.
Visual Example 1
As you learned in the square of a number post, square numbers are named precisely because we can represent them in square form, for example, we can represent 3 squared with 9 squares placed in 3 rows of 3, like this:
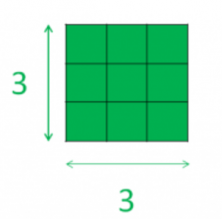
So, we have calculated the square root of 9 as 3, we can see the root of 9 as the side of a square of 9 squares, and that side is 3, as you can see in the previous drawing.
Chess challenge
I now challenge you to calculate the number of pieces each player in a game of chess has. I bet you can solve it easily.
If we know that the board is square and has 64 squares, to know how many squares the board has in each row we need to calculate the root of 64.
That is, we look for the number that multiplied by itself (or squared) gives us 64. And that number is 8. So the board has 8 squares in each row (if you look at the drawing of the board that there is below in this post, it has 8 squares on each side).
Now we know that the pieces of a player occupy 2 rows of the board, so we need to multiply the number of squares of a row by 2. Do you already have the answer to the challenge? Of course! Then each player has 16 pieces in the game of chess.
If you look at the following drawing you will see that it is very easy to understand all those calculations that we have done to solve the challenge.
Visual Example 2
If you want to visualize the root of 100, here I leave you a very colorful square divided into 100 squares, which has 10 of those squares on each side, so the root of 100 can be found to be 10.
What did you think of this post? Has it been easy to learn to calculate square roots?
If you want to continue learning and practicing more primary math, go to Smartick and try our method of learning for free.
Learn More:
- The Square of a Number and Exponents
- Representing Powers with Rods
- Notable Identities (Equalities or Notable Products)
- The Chessboard
- How to Calculate Perimeters: Part 1
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.