Numerical Place Values
What are the numerical place values? Why does a number’s value change according to its position? We’ll explain everything you need to know here about understanding mathematical algorithms by working with numerical place values.
In this post, we are going to learn what numerical place value is, why it’s important and how to use it.
Place value is the value that a digit is given according to the position it has in a given number (ones, tens, hundreds…).
Thanks to the place value, if a digit changes its place in a number, it changes the total value of that number.
Thus, when solving these problems and teaching them, we can use just the numbers themselves or their place values. The latter, using place values, can help explain the traditional way how these algorithms work.
For example, we can divide while keeping the numerical place values in mind:
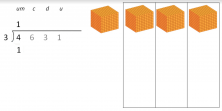
We are going to solve 4631 / 3
- “We take 4 and divide it by 3.” This means that we are taking 4000 (4’s number value) and are dividing it into 3 equal groups.
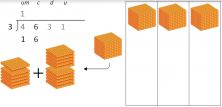
 2. “1 is leftover and we move on to the 6; so, 16 divided by 3.” This means that we are going to try to divide 1000, that we couldn’t divide before, along with the 600 that we now have, in order words, we are dividing 1600 into 3 groups.
2. “1 is leftover and we move on to the 6; so, 16 divided by 3.” This means that we are going to try to divide 1000, that we couldn’t divide before, along with the 600 that we now have, in order words, we are dividing 1600 into 3 groups.
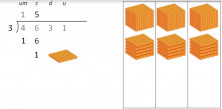 3. “1 is leftover and we move on to the 3; so, 13 divided by 3.” This means that we are going to try to divide the 100 that we couldn’t divide before, along with the 40 that we now have, in other words, we are dividing 130 into 3 groups.
3. “1 is leftover and we move on to the 3; so, 13 divided by 3.” This means that we are going to try to divide the 100 that we couldn’t divide before, along with the 40 that we now have, in other words, we are dividing 130 into 3 groups.
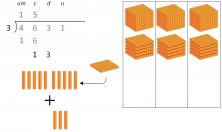
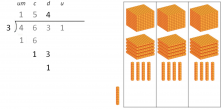
4. “1 is leftover and we move on to the 1; so, 11 divided by 3.” This means that we are going to try to divide the 10 that we couldn’t divide before, along with the 1 that we now have, in other words, we are dividing 11 into 3 groups.
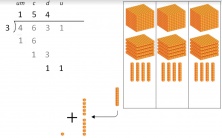
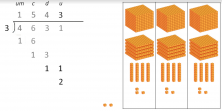
5. “And the rest: 2.” This means that, after all the dividing, we are left with 2 ones that we can’t divide into our 3 groups.
By using this method, working with the numerical place values that make up the numbers we are working with, we can understand every step that makes up the traditional algorithm of division. And we can apply it.
It’s the same story for algorithms of other mathematical operations like addition, subtraction or multiplication.
Did you find this post about numerical place values interesting? Sign up for Smartick and try out for free.
Learn More:
- Is It Good to ¨Mix¨ Alternative Algorithms, Such as ABN, with Traditional Ones?
- Dividing a Decimal by a Whole Number
- Division Exercises: Learning the Concept of Division
- Learn How to Solve Division with Decimal Numbers
- Learn How to Divide with 3-Digit Numbers







