Today we will practice estimating fractions! We’re going to look at the types of problems below:
Problem 1: Estimating Fractions.

To get a better idea, we’re going to represent the fractions with bars.

Let’s start with the first fraction.
We can see that the fraction is much closer to 0 than it is to 1. If we divide 2 / 18, we get a number that’s certainly much closer to 0, 0.111…
The second fraction is closer to 1. We need to divide again to see if it’ll give us a number closer to 1, 0.9090…

The last fraction, the improper fraction, is very close to 2. By testing it out and dividing, we can see that upon dividing 27 by 14, we get a number closer to 2, 1.9285…

We need to pay close attention to the relationship of the numbers in the fraction. The numerator and denominator determine if the fraction is proper (a smaller numerator tan denominator, therefore less than 1) or improper (a greater numerator tan denominator, therefore bigger than 1).
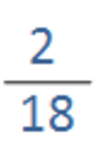
In this example, it’s a proper fraction that has quite a big difference between the numerator and denominator. In these situations, we can estimate that the fraction is closer to 0.
In the second fraction, the difference between the numerator and denominator is small. In these situations…
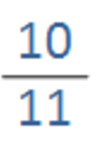
…the fraction is probably closer to 1, regardless of it being improper or proper.
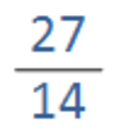
Lastly, we have an example of improper fractions that have a big difference between the numerator and denominator. In these situations, we can assume that the fraction is a number bigger than 1. In this example that we have here, the difference is almost double which leads us to estimate the fraction’s value as 2.
If the difference is close to triple, we’d guess that the fraction’s value is around 3; if it was quadruple, we’d guess 4; and so on and so forth.
However, remembering where the unit bar is on the number line is a huge help in estimating fractions.
Problem 2: Adding fractions.

These problems work with adding the estimations of fractions. We need to first estimate each fraction’s value and after, add the results.
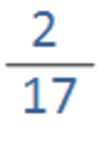
This fraction is a proper fraction that has a big difference between its numerator and denominator, therefore, as we explained above, we can estimate its value as 0.
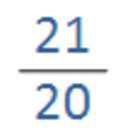
In this other example, the difference between the two is very small, so we can estimate that the fraction’s value is 1.
Now we can go on to add the two estimates: 0 + 1 = 1.
I hope that this explanation was helpful for learning how to estimate fractions.
To practice estimating fractions, sign onto Smartick and try it for free.
Learn More:
- Types of Fractions: Proper, Improper, Fractions Equal to One
- Understand What a Fraction Is and When It Is Used
- Practice Adding Fractions with Examples
- Two Ways of Dividing Fractions and Some Examples
- Learn and Practice How to Subtract or Add Fractions







