In today’s post, we are going to see how to use an area model to solve a multiplication problem with fractions. This methodological strategy is very effective to show our students an operation that is very complicated to visualize.
Teachers usually make an effort to support their explanations with manipulatives and visuals, because if they choose them well and know how to use them, they really enhance the teaching-learning process.
Based on this paradigm, there are more obvious and easy-to-apply situations. As a very typical example, we can think of the sum of two fractions with a common denominator.
"Max ate 2/3 of a pizza and Sofía ate 1/3. How much pizza did they eat between the two of them?"
Students can easily outline the situation and solve it with support from the picture.
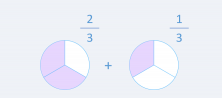
In other words, by seeing the simple outline of the problem it is evident that 2/3 + 1/3 = 3/3.
But when it comes to the multiplication of fractions this is not the case. Not only is it difficult to find a visual scheme that supports the calculation, it is also hard to come up with an everyday life situation in which to contextualize the operation. Think about it…
I guess you’ll get bored thinking about it over and over again. The bottom line is that it’s not easy at all. Fortunately, I have an example that always works and that helps you to visualize the multiplication of fractions with an area model.
Multiplication of fractions with an area model
"Jon bought a green tablecloth that measures 2/3 of a foot long and 1/2 of a foot wide. How many square feet is the tablecloth?"
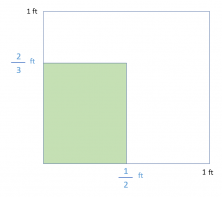
We have the outline, and now we will solve it visually.
The first thing we do is divide the unit according to the denominator of the fraction that indicates the width of the tablecloth. (1/2).
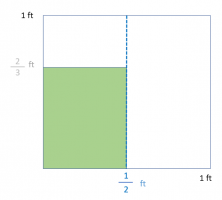
To continue, we divide the unit referring to the denominator of the fraction which indicates the length of the tablecloth (2/3).
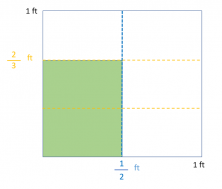
All that is left is to count the number of parts that the unit has (6) and those that are marked (2). With that, we already have the fraction which is the result of the multiplication problem 2/3 x 1/2 = 2/6.
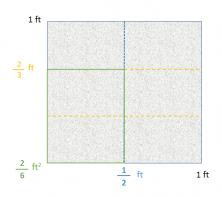
This is how you visually solve a multiplication problem with fractions using an area model.
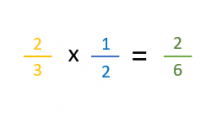
I hope that from now on you will be able to find and solve examples of multiplication problems with fractions more easily.
If you would like to know more about this or other ways of solving problems or operations, don’t hesitate to register with Smartick and try our method for free.
Learn More:
- Equivalent Fractions
- Using Mixed Numbers to Represent Improper Fractions
- Learn How to Divide Fractions with Two Different Methods
- Using the Number Line to Compare Fractions
- Learn New Methods for Dividing Fractions
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.