In today’s post we’re going to introduce a very important concept related to solving operations with fractions: homogeneous and heterogeneous fractions.
To start off, we’re going to go over the the terms that make up a fraction. The term that indicates the number of parts we divide the unit into is called the DENOMINATOR.
The term that indicates the number of parts we divide the unit into is called the DENOMINATOR.
The term that indicates the number of parts we are referring to is called the NUMERATOR.
Now we’ve clarified that, we’re going to look at the relevance of the denominator to understanding the concept of homogeneous or heterogeneous fractions.
First of all, it’s a concept that defines a type of relationship that exists between two or more fractions, which depends on the denominator of those fractions. Therefore, we can say:
Two fractions are homogeneous when their denominators are the same. So, what does that mean?
For two fractions to be homogeneous they must have the same denominator, which means the unit is divided into the same number of parts. Therefore, its denominators are equal.
For example:
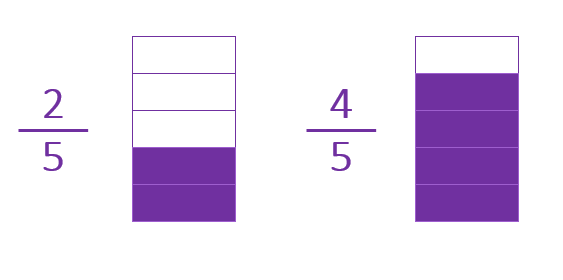
These two fractions are different, but their denominator is the same.
Therefore 2/5 and 4/5 are homogeneous fractions.
Two fractions are heterogeneous when their denominators are different. And, what does that mean?
Two fractions are heterogeneous when the unit of each one is divided into a different number of parts and therefore, their denominators are different.
For example:
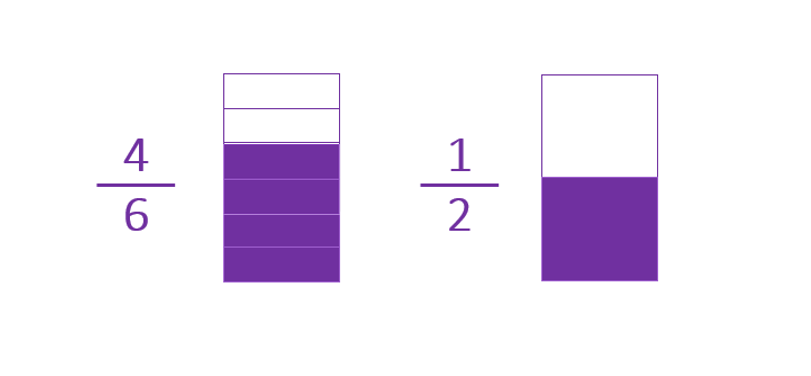
These two fractions are different and they also have different denominators.
Therefore 4/6 and 1/2 are heterogeneous fractions.
At first it might seem that this information isn’t relevant, but, when making calculations between fractions, whether the denominators are different or not can make our work difficult, as you can see in this post on adding fractions. In order to add and subtract fractions, their denominators must be the same. Therefore adding or subtracting homogeneous fractions is easier, given that they already have the same denominator.
If you want to keep learning interesting things like this, sign up for Smartick and try it for free.
Learn More:
- Adding and Subtracting Fractions: Why Do They Need the Same Denominator?
- How to Add 3 Fractions with Different Denominators
- Adding Fractions with the Visual Aid of Rectangles
- What Is a Fraction? Learn Everything There Is to Know!
- Understand What a Fraction Is and When It Is Used








Thank you very much for sharing your knowledge and method. It is very useful for me.
Indeed!