Today we will look at the classification of fractions: What types of fractions are there?
We can classify them according to the relationship between the numerator and denominator.
Index
Proper Fraction
Those representing a number less than 1. And how are these fractions identified? All fractions that represent numbers less than 1 are characterized by having a numerator lower than the denominator. For example:

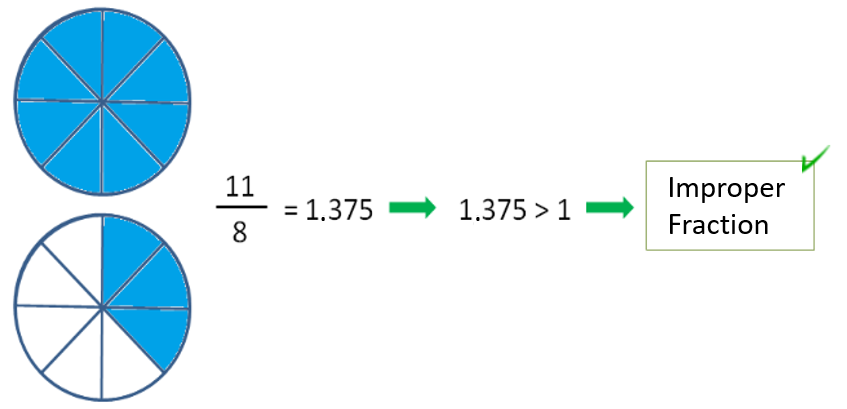
Improper Fraction
Those that represent numbers greater than 1. And how are these fractions identified? All fractions that represent numbers greater than 1 are characterized by a numerator greater than the denominator. For example:
Fractions equal to one
Those whose value equals 1. They are characterized by the numerator and denominator being equal.
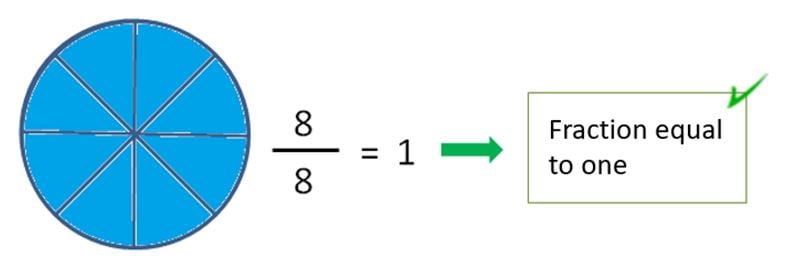
Examples of Fraction Classification
Let’s look at some examples of classifying fractions:
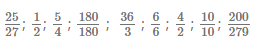
\( \frac{25}{27} \) < 1 because the numerator is less than the denominator: It is a proper fraction.
\( \frac{1}{2} \) < 1 because the numerator is less than the denominator: It is a proper fraction.
\( \frac{5}{4} \) > 1 because the numerator is greater than the denominator: It is an improper fraction.
\( \frac{180}{180} \) = 1 because the numerator equals the denominator: It is a fraction equal to one.
\( \frac{36}{3} \) > 1, because the numerator is greater than the denominator: It is an improper fraction.
\( \frac{6}{6} \) = 1 because the numerator equals the denominator: It is a fraction equal to one.
\( \frac{4}{2} \) > 1 because the numerator is greater than the denominator: It is an improper fraction.
\( \frac{10}{10} \) = 1 because the numerator equals the denominator: It is a fraction equal to one.
\( \frac{200}{279} \) < 1 because the numerator is less than the denominator: It is a proper fraction.
What did you think of this post? Did this help you to better understand the classification of fractions? If you would like to learn more about elementary math, don’t hesitate to register with Smartick and try our method for free.
Learn More:
- Practice Estimating Fractions with Examples
- Understand What a Fraction Is and When It Is Used
- Subtracting Fractions Exercises with Common and Uncommon Denominators
- Using Lego Blocks to Help with Addition of Fractions
- Understanding Fractions: “If the Whole Is Made of 8 Parts, How Can I Have 11?”







