What’s a fraction? It’s not an easy question to answer. Despite it being such a familiar element, fractions have various meanings, which makes it tricky to define and in turn, teach, and understand.
Fractions can be interpreted in no less than five ways; we’ll look at those ways in this post. The different meanings of the word fraction.
1. Fraction: Relationship between the Part and the Whole
It’s the simplest interpretation and it’s obvious to children; it’s the use of a fraction to refer to a part of a whole:

It’s a common interpretation and thus, it’s usually the starting point for teaching sequences but it raises a problem when improper fractions are introduced: “How am I going to take more pieces than what’s there?”.
But at the same time, it’s very representative. It relates a lot to real-life elements and situations and is relevant for children which makes modeling easy. Modeling is very important in the first levels of didactic sequencing for understanding what is being done and modeled.
2. Fraction: Points on the Number Line
In relation to teaching improper fractions, the infiniteness of the number line turns out to be a very handy resource: “Okay, now I can take more pieces because after 1, there’s 2, and then 3…and until infinity!”.
Let’s take look at an example, what does a point on the number line mean?
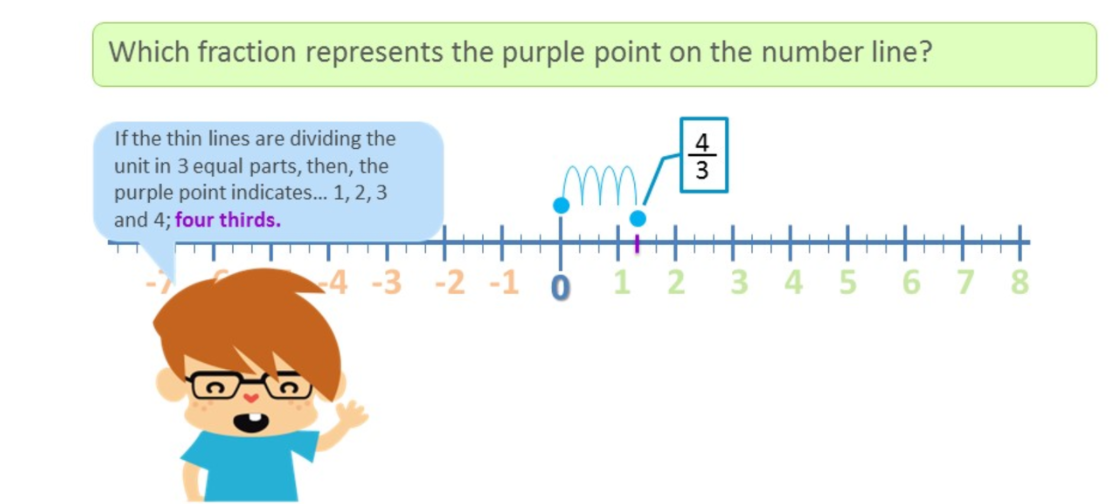
Problem – What fraction is being shown by the point on the number line? Screen – Number line with sectors that divide the unit into thirds; the purple point is placed at the first line after the unit.
Answer – The finite lines divide the unit in 3. The purple point marks…1, 2, 3 and 4; four thirds.
3. Fraction: Multiplier
When we begin to work with fractions, especially multiplying them (a difficult operation to teach because “__ times more” makes the number “__ times smaller”). Multipliers are an element that, when applied to a number, affects its value in the following way: “If I apply ½ to 6, 6 becomes 3”. This is taught during very basic levels of comprehension when students still don’t understand that ½ of 6 is ½ x 6 and, even less, the fraction as a division problem. In a small way, it’s a way for students to understand what they’ll be learning in the future as functions:
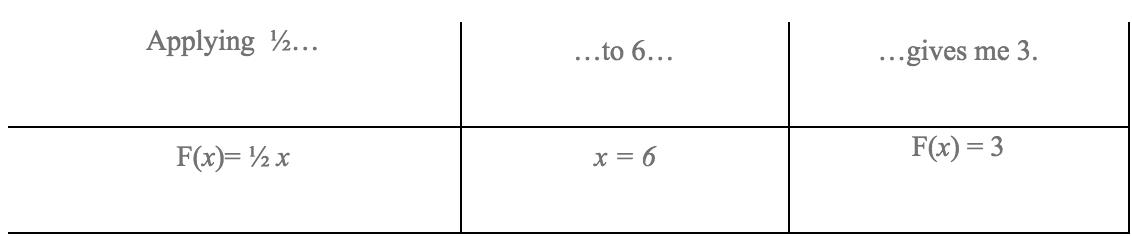
4. Fraction: Ratio
The ratio consists of understanding fractions as an expression of a relationship that exists between quantities. It refers to understanding fractions as a numerical expression: “For every x there’s y”.
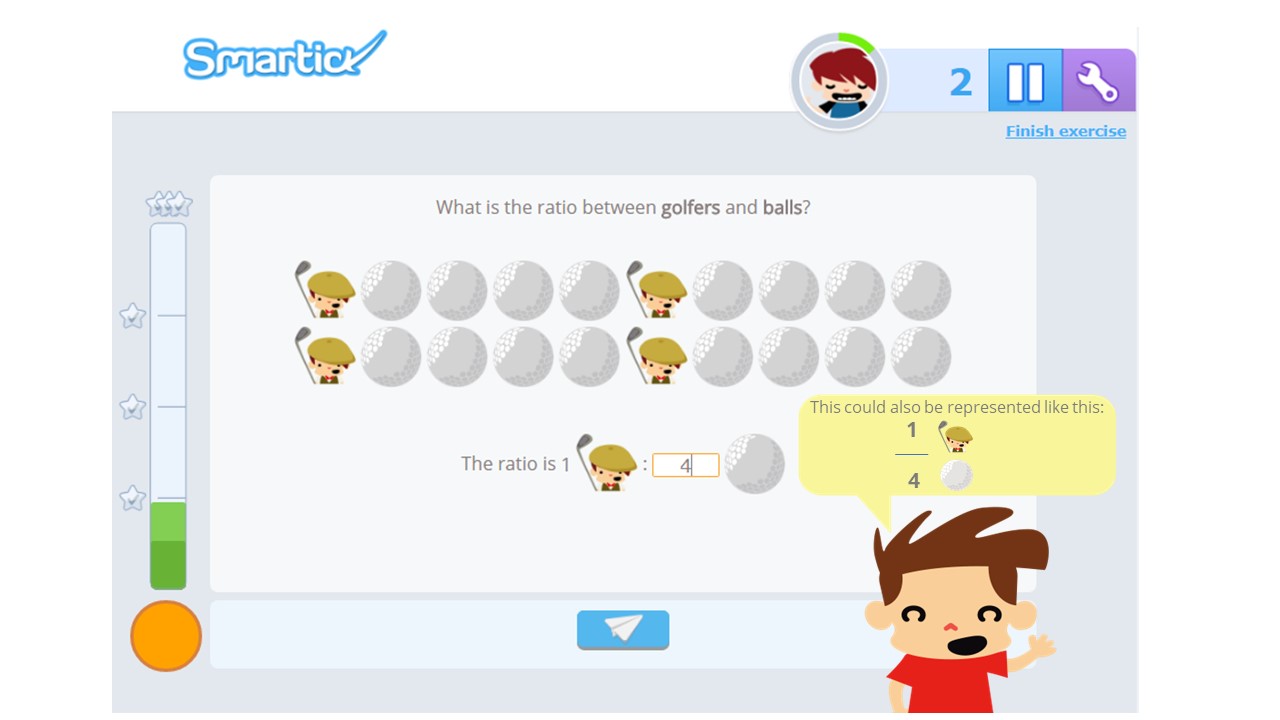
The boy expressed the relationship that exists between quantities by using a fraction:
For every ball, there are 4 golfers, it can be expressed as ¼.
Furthermore, this interpretation of fractions makes for a great introduction to the concept of scaling: “for every cm that I measure the map, there are 1000 cm in real life”.
5. Fraction: Quotient
Understanding fractions as a quotient is the most difficult to grasp and it consists in making an analogy between division and fractions. The difficulty arises from the fact that fractions are conceived as numbers, while divisions are an operation.
So then, the different ways to interpret fractions were ordered according to their difficulty, which is important to keep in mind when you teach them. Remember that the general tendency for difficult math content is to contextualize it and abstract it, that is to say, switching over from a concrete idea to one that is more general:

At Smartick, you’ll even be able to learn the properties of fractions and a ton of basic math concepts while working on exercises designed for you. Try it for FREE!!
Learn More:
- Understanding Fractions: “If the Whole Is Made of 8 Parts, How Can I Have 11?”
- Equivalent Fractions on a Number Line
- Using the Number Line to Compare Fractions
- What Is a Fraction? Learn Everything There Is to Know!
- Homogeneous and Heterogeneous Fractions







