Learn to Compare Fractions
With Ease
Welcome to the enchanting world of fraction comparison! Fractions are fascinating mathematical entities that allow us to understand and express parts of a whole.
Learn to Compare Fractions
With Ease
Welcome to the enchanting world of fraction comparison! Fractions are fascinating mathematical entities that allow us to understand and express parts of a whole.


No credit card required

No credit card required
Learn to Compare Fractions with Smartick
What is a fraction?
How to Compare Fractions?
Why is Comparing Fractions Important?
Equivalent Fractions
Comparing Fractions with Same Denominators
Comparing Fractions with Unlike Denominators
Decimal Method of Comparing Fractions
Comparing Fractions Using Cross Multiplication
Comparing Fractions Using Visualization
What is a Fraction?
Before we delve into comparing fractions, let’s refresh our understanding of what fractions are. A fraction represents a part of a whole or a division of something into equal parts. It consists of two components: the numerator and the denominator. The numerator tells us how many parts we have, while the denominator tells us the total number of equal parts in the whole.
How to Compare Fractions?
Comparing fractions is all about determining which fraction is greater or smaller. To make this determination, we need to consider the numerator and denominator of each fraction. By examining these components, we can establish relationships, compare denominators and draw conclusions about their values. There are various methods, models and techniques to compare fractions, each with its own charm and usefulness.
Why is Comparing Fractions Important?
Understanding the importance of comparing fractions is crucial in many real-world scenarios. Be it dividing a chocolate bar among friends, determining who ran a longer fraction of a mile, or figuring out discounts during shopping, the comparison of fractions aids in making fair and accurate decisions. As we learn and we grow, this skill becomes essential in more complex situations such as financial planning, engineering designs, and statistical data analysis.
Equivalent Fractions
Equivalent fractions represent the same value or proportion, even though they may look different. In essence, two fractions are equivalent when they are the same size, or the same point on a number line, even if their numerators and denominators differ. This can be understood by multiplying or dividing both the numerator and denominator of a fraction by the same nonzero number. For instance, the fraction 1/2 is equivalent to 2/4, 3/6, or even 50/100. All these fractions represent the same quantity, just expressed in different terms. Recognizing equivalent fractions is fundamental in understanding the relationship between different fractions and simplifying them.
Comparing Fractions with Same Denominators
When comparing fractions with two numerators and the same denominator, it’s like comparing pieces of a puzzle. The fraction with the larger numerator represents a larger piece of the whole. For example, when comparing 3/5 and 4/5, both fractions have the same denominator of 5. Since 4 is a greater numerator than 3, we can conclude that 4/5 is larger than 3/5.+
Comparing Fractions with Unlike Denominators
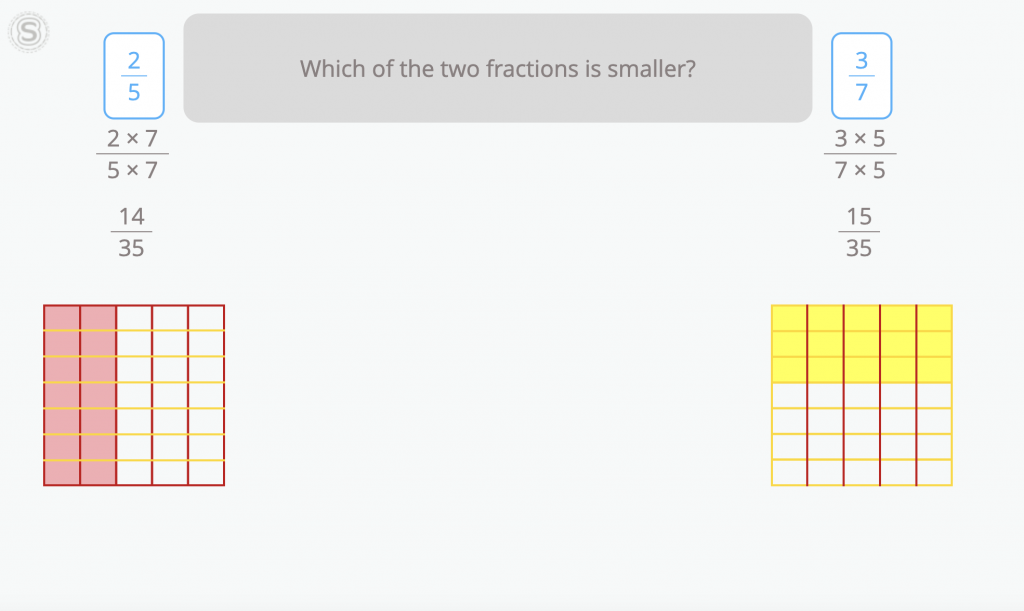
Comparing fractions with unlike but different denominators, is like comparing apples and oranges. To make a fair comparison, we need to find a common ground. This can be done by finding a common denominator. Once the two fractions have the same denominator, we can apply the same principles as in comparing fractions with the same denominator. For instance, to compare 2/5 and 3/7, we can convert them to fractions with the same denominator, such as 14/35 and 15/35. Now, it’s clear that 14/35 is smaller than 15/35.
Decimal Method of Comparing Fractions
Another engaging method to compare fractions is by converting them into decimals. Converting fractions to decimals provides a visual representation of their values on the number line. Fractions with smaller values will have smaller decimal representations, while fractions with larger values will have larger decimal representations. For example, comparing 1/2 and 2/3, we note that when converted to decimals, 1/2 becomes 0.5, and 2/3 becomes approximately 0.67. It’s evident that 2/3 is a larger fraction than 1/2.
Comparing Fractions Using Cross Multiplication
Cross multiplication is a powerful tool to compare fractions quickly. To use this method, we multiply the numerator of one fraction by the denominator of the other fraction. The fraction with the larger product of multiply numerator is the greater fraction. For example, when comparing 3/4 and 5/6, we cross the multiply numerator by multiplying 3 by 6 and 5 by 4. The result is 18 and 20, respectively. Therefore, 5/6 is greater than 3/4.
Comparing Fractions Using Visualization
Different graphical techniques can help us understand the magnitude of fractions. Look at the illustration below, which presents Model A and Model B depicting two different fractions. It’s clear to see that 4/8 is less than 4/6, as 4/6 has a more extensive shaded region than 4/8. The fraction with bigger numerator and a smaller value takes up a smaller portion of the same whole figure. It’s crucial to ensure that the sizes of Model A and B are identical to make a valid comparison. Each model is divided based on its denominator into equal sections.
FAQs: Comparing Fractions
1. What does it mean to compare fractions?
– Comparing fractions means determining which fraction is larger, smaller, or if they are equivalent in value.
2. How can I tell which fraction is larger if they have the same numerator?
– If two fractions have the same numerator, the fraction with the smaller denominator is larger. For example, between 1/3 and 1/4, 1/3 is larger.
3. What if they have the same denominator?
– If fractions share the same denominator, the one with the larger numerator is greater. For instance, 3/5 is larger than 2/5.
4. Can I compare fractions with different numerators and denominators directly?
– Directly comparing such fractions can be challenging. It’s often easier to either find a common denominator and convert the fractions or to convert them to decimals or percentages.
5. What is a common denominator and why is it useful?
– A common denominator is a shared multiple of the denominators of two or more fractions. By converting fractions to have this common denominator, you can easily compare or add/subtract them. For example, for 1/4 and 2/3, the common denominator is 12.
6. Are there tools to help compare fractions visually?
– Yes, there are several tools and methods. Fraction bars, pie charts, and number lines are common visualization tools. For instance, shading parts of two equal rectangles can help in comparing two fractions based on the shaded area.
7. Can I use decimals to compare fractions?
– Absolutely! Converting fractions to decimals often makes comparison straightforward. For instance, when comparing 3/4 (0.75) and 2/3 (0.67), it’s clear that 0.75 is larger.
8. Are there any shortcuts to compare fractions without finding a common denominator?
– Yes, you can cross-multiply. For fractions a/b and c/d, if a*d > b*c, then a/b is larger. If a*d < b*c, then c/d is larger.
9. What are equivalent fractions and how do they relate to comparing?
– Equivalent fractions represent the same value. For example, 1/2 and 2/4 are equivalent. Recognizing equivalent fractions is crucial when comparing, as you’ll see they have the same value.
10. Is it possible for two different fractions to be equal in value?
– Yes, as mentioned above, fractions like 1/2 and 2/4 are different but represent the same value. They are termed as equivalent fractions.
Remember, practice makes perfect! The more you have students work with fractions, the easier it becomes for students to compare and understand their relationships.
