Today we’re going to find out why, when we’re adding and subtracting fractions, they need to have the same denominator.
If you didn’t already know, when we’re adding and subtracting fractions, they must be homogeneous. You can read more about homogeneous and heterogeneous fractions in this post.
It’s really easy to understand using visual aids, which we’ll take a look at below. The real reason is due to the definition of the fraction itself, which is a representation of parts of a total which must be the same size.
When you add or subtract fractions, you can’t express the result as a fraction if you do not divide the total into equal parts.
Adding fractions
For example, if you want to add 1/2 + 1/3
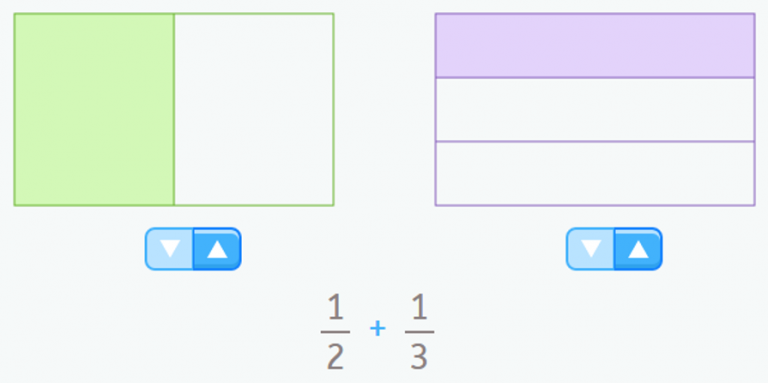
We have:
- 1 of 2 equal parts of a whole unit (in green in the image).
- 1 of 3 equal parts of a unit (purple in the image).
To do the addition, we have to take the colored parts into account. Since each part is a different size, we can’t express this quantity in the form of a fraction.
We have 3 parts (1 represented by a green rectangle and 2 represented by purple rectangles), but they are not the same size.
So what can we do? We can express the fractions we want to add in the form of a fraction that allows us to consider them parts of the same size.
As you can see in the following images, you can express the fraction 1/2 as 3/6 and the fraction 1/3 as 2/6.

Now we’ve got the quantities that we want to add expressed in the form of fractions that have parts of the same size!
Now we can count the colored parts and express them in the form of a fraction. There are five equal parts: 5/6.
So 1/2 + 1/3 = 5/6.
Subtracting fractions
Now, if we to try subtract, for example, 1/2 and 1/3, we get the same problem. To subtract 1/3 from 1/2, we need to take away parts that are the same size as the ones we have.
So, we need to express both fractions homogeneously, and then we can take away the parts indicated by the subtraction.
If we express 1/2 as 3/6 and 1/3 as 2/6, to subtract 1/2 – 1/3, we take away 2 of the 3 equal parts of 3/6, and we get 1 part, or 1/6. So, we find that 1/2 – 1/3 = 1/6.

It’s easy to understand why the denominators must be the same when we’re adding and subtracting fractions, isn’t it?
If you liked this post, share it so others can learn too!
With Smartick, you can learn more about fractions and other mathematical concepts, and work on exercises that adapt to each student in real time. Try it FREE!
Learn More:
- What Are Decimal Numbers?
- Understand What a Fraction Is and When It Is Used
- Subtracting Fractions Exercises with Common and Uncommon Denominators
- Homogeneous and Heterogeneous Fractions
- Getting to Know Rational Numbers and Their Properties








Excellent👏 thanks 🙏
I wanted to teach addition and subtraction of fractions to kids and I was going bonkers on how to explain the theory behind the necessity of having a common denominator. This post helps me a lot.
Wonderful explanation !!!
Visual representation makes it easy for kids to understand,would be great if you can support with some real life examples .