Today we are going to solve incomplete horizontal addition and subtraction exercises by using different strategies.
In mathematics, it is important to know how to use different strategies for solving the same problem or exercise. Knowing various strategies, how to apply them, and knowing when is the best time to use each, is what we call mathematical flexibility. In order to develop mathematical thinking, flexibility is fundamental.
You will find it easy to solve equality exercises with addition and subtraction. But we will try to show you that the important thing is to face these exercises with the help of mathematical flexibility.
First Exercise with Incomplete Horizontal Addition and Subtraction
We want to solve the following equality exercise:
![]()
One option is to operate the numbers in order to simplify the exercise. We can change the order of operations and add 22 + 5 first. Since we know that 22 + 5 = 27, we would then have to solve…
![]()
This equality exercise is much easier because we know that we just have to subtract 7 from 27 in order to get 20. Therefore, whenever we can use an operation to simplify an exercise, it will go a long way.
Another option to solve this exercise is to make estimates with simple numbers. For example, if we put 10 in the empty box, we will have: 22 – 10 + 5 = 17.
We haven’t come up with the result we expected, but we got very close. We have taken away 10 and the result given is less than what we wanted, 17 instead of 20. Therefore we will have to take away a number lower than 10 in order for the result to be greater. Instead of 10, we can take away 7, because we know that we were off by 3. Now, let’s check the result:
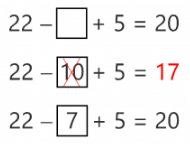
Second Exercise with Incomplete Horizontal Addition and Subtraction
We are going to see another example of incomplete horizontal addition and subtraction. For this example we are going to try to solve the following equality exercise:
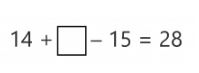
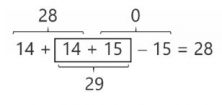
In order to solve equalities of this type, it is a good idea to use simple number relationships that we already know. For example, when you look at the 14 and 28, I’m sure that it has occurred to you that 14 + 14 = 28. It seems like, if we put 14 in the box, we would be very close to 28 but…then we need to subtract 15! What can we do? Well, the solution would be to put 14 in the empty box to get 28 and add 15 more to compensate for the 15 that we will subtract. In the end, we will realize that by adding 14 + 15 = 29 we have reached our goal.
We can also simplify the equality exercise. To do this, we must first change the order of operations. We are going to have to add 14 and subtract 15 from the number in the empty box. However, adding 14 to a number first and then subtracting 15 from it is the same as taking away 1.
If we think in these terms we will see that we only need to find one number that, by taking away 1, will give us 28 and … that’s easy!
Again, we see that doing operations or organizing calculations differently can help us make an exercise much simpler.
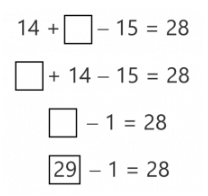
We hope that the ideas we have given you in this post help guide you in solving other incomplete horizontal addition and subtraction exercises. More than anything, we hope to have helped you develop your mathematical flexibility. From now on, when you come across an exercise, ask yourself if you can solve it in different ways. Which would be the easiest? Don’t ever think that there is only one way to solve a problem. Or that ‘doing it your way’ is not valid. There is great value in developing your own strategies for thinking about math problems.
In our daily math sessions at Smartick, we strive to teach different strategies to solve every piece of content that we present. If you would like to know more about our method, log in to Smartick and try it for free.
Learn More:
- Strategies for Solving Incomplete Horizontal Additions and Subtractions
- Mental Calculation: Horizontal Addition and Subtraction
- Smartick Logic Exercises with Operators
- Discovering Subtraction and Addition Tables
- Learn to Subtract with Remainders







