In today’s post, we are going to learn two methods to solve multiplication problems that are different from the ones we are used to using.
First, we are going to travel to Russia where we will learn how to multiply using the Russian Method. Then, we will continue on to India to learn the Hindu Method.
In both cases, we are going to use the same multiplication problem as an example: 34 x 21.
Russian Method
This method is based on the decomposition of base 2 numbers. Although explaining it may make it seem like it is difficult, you will see how easy multiplication is with this method, you just have to follow the steps below.
- First, make a table:
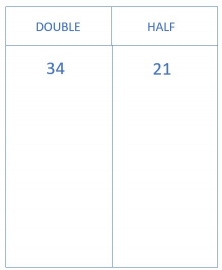
- Then, place the factors you want to multiply (34 and 21):
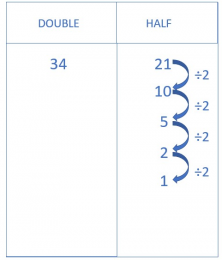
- Next, you will divide the number in column on the right (21) by 2. You will continue dividing the result by 2 until you reach the number 1. Be careful! By dividing by two the odd numbers will have remainders but we are only going to use the quotient.
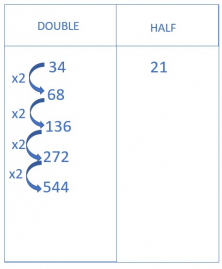
- And now double the factor in the column on the left (34) by multiplying by 2. You need to multiply as many times as you have divided in the column on the right.
- Your table will look like this:
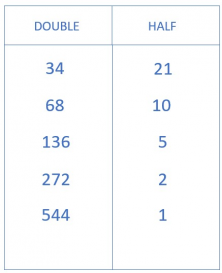
- The next step is to cross out the rows where the number on the right is even.
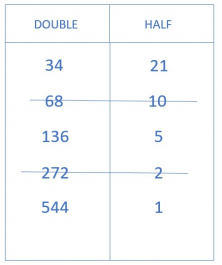
- Finally, add all the numbers in the left column that are not crossed out.
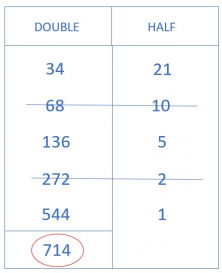
- There you have it! And you can see that you have 34 x 21 = 714. It seems like magic, doesn’t it?
Hindu Method
How do you solve multiplication problems with this method? We’re going to see this step by step as well.
- First, make a table like this:
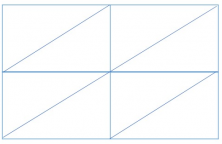
- Place the factors (34 and 21) in the following way. The table will have as many columns and rows as digits that the factors have.
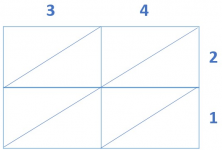
- Now you can begin to multiply! Let’s go step by step. First, multiply 3 x 2 and look closely at how to place the result. Since it is 6, a single-digit number, it is important that you remember to place the 0 first.
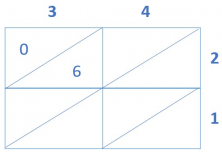
Do the same with the rest of the numbers.
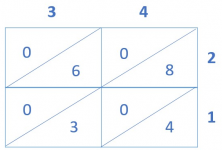
- You’re almost done. Look closely at the diagonal lines and add the numbers.
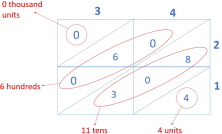
We have:
– 0 thousand
– 6 hundred
– 11 tens
– 4 units
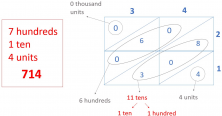
- Now separate the 11 tens into 1 hundred and 1 ten, then add the ten to the 6 that you already have.
And you’ve solved 34 x 21 = 714.
If you would like to learn other alternative methods for multiplication don’t forget to check out this earlier blog post.
And if you would like to keep learning primary mathematics, register online with Smartick and try it for free.
Learn More:
- Different Methods of Multiplication
- How to Multiply by 2 and 3 Digit Numbers
- Learn Multiplication Algorithm Using Blocks
- Understanding Division with the Help of Geometric Visualization
- What is Multiplication: Steps to Learn and Understand Multiplication








i hate hindu method