What’s an angle? Right, obtuse, straight, acute angle… what are these and what do they have to do with angles? If they can be measured… how can we measure them? What are they used for? …These are some of the questions that we’re going to answer in this post. So…let’s do this!
Angles: An area marked by two line segments with the same origin.
This is the mathematical definition but let’s take a closer look. Angles aren’t anything new, we’re surrounded by them; we can find them in our everyday life: at home, at the park or on the school playground, on a mountain or a beach, in the city…even on animals, plants and on ourselves!
Now that we’ve clarified what angles are in addition to knowing how to identify them, we need to define their elements because that’s what allows us to analyze and reproduce them. As you can see in the picture above, they’re composed of the following elements:
a: Side one, or in other words, one of the line segments that create the angle. Together with the other side, it marks out the angle’s amplitude.
b: side two; it shares the same origin as the other side (a), and completes the angle and marks out its amplitude.
C: Vertex. It’s the common origin of both line segments.
α: Amplitude of the concave angle formed by the line segments.
β: Amplitude of the convex angle formed by the line segments.
The sides are line segments and, thus, have an infinite length. However, when we draw them, we need to draw an ending point so that they can fit on the paper. The vertex always has the same dimensions because it’s a point, the origin of the line segments whose only variability depends on the coordinates on the grid. So, the amplitude is the angle’s only element that varies and, thus, determines its characteristics; that’s why it’s so important to know how to measure it.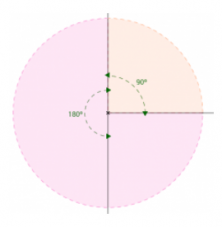
We classify the different angles according to their amplitudes.
So, we can find right angles, those that measure an exact 90º, straight angles, which are angles that measure exactly 180º and, aside from these two, we can classify the others:
- Acute angle: angles that are less than 90º.
- Obtuse angle: angles that are greater than 90º.
- Concave angle: angles that are greater than 180º
- Convex angle: angles that are less than 180º
To measure amplitudes, we use a tool called a “compass”, but there are many other ways that we can use to measure and draw different kinds of angles:
- A circumference with a known center allows us to draw straight angles, just as the Egyptians did when such tools didn’t exist.
- All right angles determine a straight angle.
- All triangles (the rulers) have the following angular measurements and, combining them differently, they can make other angles. The triangle has a right angle, a 60º angle, and a 30º angle. The other kind has a right angle and two 45º angles.
And that’s how we discovered angles. They are a part of everyday life and we learned that we can do more than observe them. We can measure them and reproduce them exactly how they are in reality.
If you liked this entry, you can keep on learning more about Geometry and other math subjects at Smartick. Make an account and try it out for free!
Learn More:
- What is an Obtuse Angle?
- What is a Straight Angle and Examples
- Introduction to Angles: Definition, Parts, and Types
- Consecutive Interior Angles: What They Are and How to Find Them With Examples
- What Is an Angle? How Is It Made?
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
I hope I can have a free access of this site. This is good for my students.
Hello Filipina! Thank you for your comment. We are happy to hear that you are interested in the Smartick method.
I want to inform you that we have a free Teacher’s page available for educators to use in their classrooms. This offers tools such as interactive tutorials and associated exercises. For more information on this, I would like to recommend that you read this blog post: https://www.smartick.com/blog/education/how-does-it-work/teaching-resources-for-math-teachers/
Moreover, in addition to our free Smartick trial, we offer special pricing to teachers and schools. Please feel free to email us at [email protected] for more information on this, or if you have any further questions 😊