Welcome to Smartick’s blog! In today’s post we are going to learn some geometry and talk about prisms: what they are, what are their principal elements, the types of prisms that exist and how we can calculate their areas and volumes.
What Are Prisms?
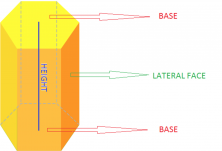
A prism is a polyhedron that has two equal, parallel sides called “bases” and its lateral sides are “parallelograms”.
What are the principal elements of prisms?
- Bases: All prisms have two bases that are equal and parallel.
- Lateral sides: Lateral sides are the parallelograms that link the 2 bases.
- Height: Height is the distance between the two bases.
What types of prisms exist depending on the base?
- Irregulars: Prisms that have irregular polygons as bases.
- Regulars: Prisms that have regular polygons as bases
The prisms are named after the base’s polygon:
- Triangle → Triangular prism
- Square → Square prism
- Pentagon → Pentagonal prism
- Hexagon → Hexagonal prism
Area of a Prism
In order to calculate the area of a prism, you need to add the area of each one of its sides. For straight prisms, you can calculate the area like this:
Area = 2 x Ab + Pb × h
Where…
- Ab is the area of the base
- Pb is the perimeter of the base
- h is the height of the prism
Volume of a Prism
In order to calculate the volume of a prism, you simply need to multiply the area of the base by the height.
Volume = Ab × h
Where…
- Ab is the area of the base
- h is the height of the prism
Now you know all about prisms and their characteristics. Do you want to continue learning about geometry and all of the elementary math topics? Register at Smartick and have fun learning math. Try our free trial with your children today!
Learn More:
- What Is a Prism? Solve These Exercises to Find Out
- Learn the Associative Property of Multiplication
- How to Calculate a Perimeter: Part 2
- Cylinder: Characteristics, Examples, and How to Calculate Their Area and Volume
- Perimeter: What Is It and How to Find It for Any Polygon
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.
I am very impress with you and I must say that I would like to learn with you.
Hi Francis,
Thank you very much for your comment.
If you want to learn more content like this and practice elementary school math, just sign up at Smartick. You have a free trial period with no strings attached.
If you have any additional questions or doubts you can write to my colleagues of the pedagogical team at [email protected].
Best regards!