In today’s post, we are going to take a look at the distributive property from a geometric point of view.
You can consult these entries for more information on this property:
Distributive Property from a Geometric point of view:
We’re going to start by drawing a striped rectangle that’s divided into two smaller rectangles, one blue and another yellow.
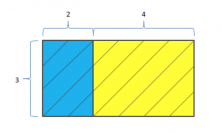
First, we’re going to calculate the area of the big striped rectangle that has a base of (2+4) units and height of 3 units.
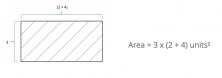
Area = 3 x (2 + 4) units²
Next, we’ll calculate the areas of the two smaller rectangles separately:
When added together, the areas of these two smaller rectangles need to give the exact same result as the area of the big rectangle, right? Let’s check:
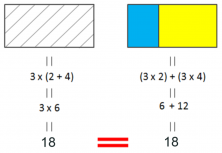
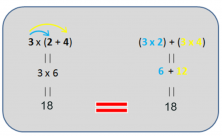We can observe that the areas are the same. And without knowing it, we’ve applied what we call the distributive property of multiplication. Let’s look at an example.
A lot of you will wonder, and the combined operations? There’s an order to do mathematical operations…
If we have 4 · (2+3), the first thing we’ve been taught to do is to calculate what is in parentheses — 2 + 3 = 5 — and after doing so, to go ahead with the multiplication 4 x 5 which brings us to the answer 20.
So then, when will we make use of the distributive property?
This property is particularly useful in algebra.
Let’s imagine that we want to solve the following equation:
5 · (x+3) = 25
Here we won’t be able to start by simplifying what is the parenthesis because we can’t add x + 3. We can, however, apply the distributive property and get:
Now all that’s left to do is to solve the equation.
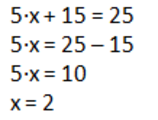
Now it’s time to practice!
I hope you enjoyed this explanation on the distributive property of multiplication in geometry and that it is helpful!
If you want to keep learning more Elementary Math, try Smartick for free!
Learn More:
- Learn about the Distributive Property of Multiplication
- How to Perform Multiplication Problems with an Area Model
- Commutative Property in Multiplication and Addition
- The Distributive Property of Multiplication
- Distributive Property of Multiplication with Examples
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.