In this post, we are going to continue analyzing the book, How I Wish I’d Taught Maths by Craig Barton, which is about evidence-based education. Today we will talk about the chapter that focuses on self-explanation which is the self-reflection that takes place when you are reading or learning something.
Effects of Self-Explanation
Self-explanation consists of making sense of what you are reading or learning. It has nothing to do with giving explanations to others or saying things out loud. It is stopping and reflecting on a single step in a solution and asking yourself: what does this mean? Why am I writing this? What is the next step? (Barton 2018)
Chi (2000) identified two important effects of applying this type of practice in student learning:
- Generate inferences. Students are able to find information that is not explicitly provided.
- Repair incorrect models. Students are able to find differences between their mental model and what is modeled by the solution.
However, students do not do this naturally and therefore it is necessary to encourage them to practice this process.
At Smartick, one thing we practice is encouraging creativity and reasoning in the minds of children through solving math problems. A large part of the math problems that we have incorporated into the method are not just about finding a quantitive solution.
For example:
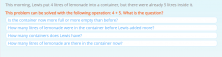



These types of problems help to fix incorrect solving strategies, such as the use of keywords to determine which operation is correct. Additionally, to solve them, the students have to infer information that is not explicitly explained in the problem.
Practices to Optimize Self-Explanation
-
Explaining if Something is Correct or Incorrect
According to Craig Barton, another practice to make self-explanation as effective as possible is explaining whether something is correct or incorrect.
The incorrect examples should be used with caution because we do not want the students to become fixated on and absorb the error rather than the correct method. However, the key result of Siegler (2002) is that ”explaining why correct answers are correct and why incorrect answers are incorrect yields greater learning than only explaining why correct answers are correct.”
At Smartick we have designed evaluation tasks that, beyond judging the correct or incorrectness of a calculation, are expected to lead students to judge the correct or incorrectness in structural terms (algebraic).
For example, using their informal knowledge of the properties of operations (commutative, associative, neutral element, etc.):

Indeed, when we implement these types of tasks and analyze the data for effectiveness, we detect difficulty even though they were not considered the most difficult in our initial predictions.
-
Self-Explanation vs Practice
Once we have become convinced of the importance of self-explanation, a rather obvious question arises:
How much time should we dedicate to self-explanation in relation to practice?
McEldoon et al (2013) attempted to provide an answer to this question. The authors compared the effectiveness of self-explanation prompts to that of solving additional practice problems in primary school math students. The students were divided into three groups. The first group solved six problems and were prompted to self-explain after each. The second group (control group) also solved six problems but were not prompted to self-explain. Finally, the third group solved twelve problems and were also not prompted to self-explain. The authors found that the first group – when compared to the control group – had greater conceptual comprehension and fluency.
However, in comparison to the group that solved more problems, the first group had greater, albeit modest, benefits. The results suggest that balance is necessary but self-explanation should not take up all the time. The pause to reflect on a result or step should not last more than a few seconds. There is no need to verbalize the reflection or discuss it either. The benefits of self-explanation are observed for as long as they allow us to consistently devote time to practice.
References:
- Glaser, R, ed. 2013. “Self-Explaining: The Dual Processes of Generating Inference and Repairing Mental Models.” In Advances in Instructional Psychology, 161–238. New York: Routledge.
- McEldoon, K.L, K.L Durkin, and B Rittle-Johnson. 2013. “Is Self-Explanation Worth the Time? A Comparison to Additional Practice.” British Journal of Educational Psychology 83 (4): 1–29.
- “Microgenetic Studies of Self-Explanation.” 2002. In Microdevelopment: Transition Processes in Development and Learning, 31–35. Cambridge University Press.
Learn More:
- Stimulation of Mathematical Talent with Smartick
- Worked Examples and Metacognition
- Learn How to Estimate a Sum with Examples
- Interleaving vs Blocked Practice to Learn Math
- Number Talks: Learn Math through Talking







