In this post, we are going to talk about the Theoretical Framework of the Singapore Method, which revolves around mathematical problem-solving.
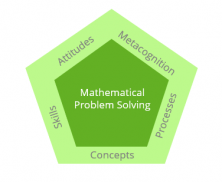
Concepts
The Singapore Method groups mathematical concepts into 6 sections:
- Numbers
- Algebra
- Geometry
- Statistics
- Probability
- Analysis
These content categories are closely related and are interdependent. In the different stages of learning, like in different programs, the extent and depth of the content varies.
Abilities
The Singapore Method works on skills like:
- Numerical calculation
- Algebraic manipulation
- Spatial visualization
- Data analysis
- Measurements
- Use of mathematical tools
- Estimation
- In addition, it also develops the ability to use spreadsheets and software to facilitate mathematics learning.
All of these skills are taught in a way that it instrumental, comprehensive, and justified.
Metacognition
Metacognition, or thinking about thinking, refers to the consciousness and the ability to control, regulate, and evaluate the processes of thought. In particular, it alludes to the selection and use of strategies to solve problems.
To develop consciousness and metacognitive strategies, students that follow the Singapore method should confront the resolution to problems as being open and non-routine. At the same time, they have to discuss their solutions, think aloud, and reflect on what they are doing – all the while maintaining an updated record on how things are progressing.
Attitudes
The attitudes consist of the affective aspects of learning mathematics, such as:
- Beliefs about mathematics and it’s usefulness
- Interest and enjoyment of learning mathematics
- Appreciation of the beauty of mathematics
- Confidence in the use of mathematics
- Perseverance in problem-solving
They are very consistent with the fact that student’s attitudes toward mathematics are shaped by their learning experiences. By making learning fun, meaningful, and relevant it helps to instill positive attitudes towards subjects.
Processes
The Singapore Method includes the following mathematical processes:
- Mathematical reasoning is the ability to analyze mathematical situations and construct logical arguments. It is a mental habit that can be developed through the application of mathematics in different contexts.
- Communication is the ability to use mathematical language to express ideas in a precise, concise, and logical way.
- Connections are the ability to see and establish links between mathematical ideas, between mathematics and other subjects, and between mathematics and the real world. All of these help students to really understand what they learn in mathematics.
- Mathematical modeling is the process of formulating a mathematical model to represent and solve real-world problems. Through mathematical models, students learn to cope with ambiguity, make connections, and select and apply appropriate mathematical concepts and skills. They also learn to identify assumptions and reflect on solutions to problems, as well as make informed decisions based on data given or compiled.
- Thinking skills, that is, the ability to classify, compare, and analyze problems in a global way.
- Heuristic thinking, is to say, the set of procedures that students use to address a problem whose solution is not an obvious one. This includes the use of representation (drawing a diagram), of conjecture (trial and error; make assumptions), to traverse the process (doing it backwards) and introducing changes to the problem (simplifying a problem; considering special cases).
References:
- Mathematics Syllabus. Primary. Ministry of Education Singapore.
- Smartick Lands in Singapore, a Country with One of the Most Challenging Education Systems in the World
- Singapore: Goals, Objectives, and Design of Its Curriculum
Learn More:
- Worked Examples and Metacognition
- Singapore: Experiences in Learning
- Teaching Principles and Learning Phases of Singapore Math
- Singapore: Goals, Objectives, and Design of Its Curriculum
- Foundations of the Singapore Method in Math Instruction
A multidisciplinary and multicultural team made up of mathematicians, teachers, professors and other education professionals!
They strive to create the best math content possible.